Determining speed at an angle using an energy balance

[BiggestAfrica]

Homework Statement

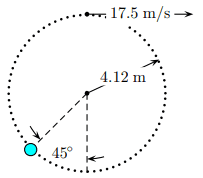
A 4.1 kg ball is spun on a thin cord in a vertical circle having 4.12 m radius. It has a speed of 17.5 m/s at the highest point of the circle. Take zero potential energy at the lowest point and use the 45 degree angle measured with respect to the vertical as shown. The acceleration of gravity is 9.8 m/s^2.

Calculate the speed of the ball at angle 45 degrees.

Relevant Equations

Ko = Kf + Uf
.5(m)(vo^2) = (.5)(m)(vf^2) + mgh

I first found the height of the ball after it's passed the 45 degree angle by doing 4.12*sin(45) = 2.9133, and plugged in the rest of the variables (masses cancel)

.5(m)(vo^2) = (.5)(m)(vf^2) + mgh
(17.5^2)(.5) = (.5)(vf^2)(9.8*2.9133)
vf = 15.7845, however this is incorrect

I don't understand where I'm going wrong, so any help would be greatly appreciated!

 

[PeroK]

Your answer is a smaller speed than it started with. Do things normally speed up or slow down as they fall?

What does your calculation $4.12 \sin(45)m$ physically represent?

 

[BiggestAfrica]

Your answer is a smaller speed than it started with. Do things normally speed up or slow down as they fall?

What does your calculation $4.12 \sin(45)m$ physically represent?

Things generally speed up, and the calculation represents the height of the ball. I also realized that there should be initial potential energy (since height is 8.24 at the initial velocity of 17.5), so I calculated the final velocity while taking initial potential energy into account, and got an incorrect velocity of 20.2646m/s (although it is now greater than 17.5).

 

[PeroK]

Things generally speed up, and the calculation represents the height of the ball.

Are you sure? Why don't you mark the height of the ball on your diagram. In what way is that $4.12 \sin(45)m$?

 

[BiggestAfrica]

Are you sure? Why don't you mark the height of the ball on your diagram. In what way is that $4.12 \sin(45)m$?

I figured it out, thanks! Mass was never used in the calculation, but I was using the wrong height for my calculations, using the height of the triangle itself rather than subtracting the height of the triangle from the radius (4.12 - 2.1933 = 1.2067).

 

[PeroK]

I figured it out, thanks! Mass was never used in the calculation, but I was using the wrong height for my calculations, using the height of the triangle itself rather than subtracting the height of the triangle from the radius (4.12 - 2.1933 = 1.2067).

View attachment 257123

A useful thing to remember is that for vertical circular motion like this, or for a pendulum, we have:
$$h = R(1- \cos \theta)$$
Where $h$ is the height above the lowest point.

Note that it works all the way round. At the top of the swing $\theta = 180$ degrees and, as expected, we have:
$$h = R(1 - (-1)) = 2R$$
This formula comes up frequently. Even if you don't memorise it, it's useful to recognise it when you see it.

Note that in this case $\sin(45) = \cos(45)$ so if that was an error on your part it didn't matter! But, it really should have been $\cos(45)$.