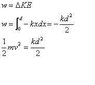Determining spring's max compression on frictionless track

[mandy9008]

Homework Statement

A 0.280-kg block along a horizontal track has a speed of 1.30 m/s immediately before colliding with a light spring of force constant 43.6 N/m located at the end of the track. What is the spring's maximum compression if the track is frictionless?

The Attempt at a Solution

mgy=1/2mv²
y=1/2v² / g
y=1/2 (1.30 m/s)² / 9.8 m/s²
y=0.086m

mgy=1/2kx²
x² = 2mgy / k
x² = 2 (.280 kg)(9.8 m/s²)(0.086m) / 43.6N/m
x=0.11m

 

[wwshr87]

Answer looks good, an alternate method is shown in the attachment.