How Does Inserting a Copper Slab Affect a Capacitor's Performance?

[stunner5000pt]

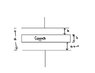
A slab of copper is thrust into parallel plate capacitor as shown in the figure.
a) What is the capacitance after the slab is introduced?
This is like two capacitors in series so
C_{1} = \frac{\epsilon_{0} A}{d-b-x}
C_{2} = \frac{\epsilon_{0} A}{x}
when added it yields \frac{epsilon_{0} A}{d-b}
Find the ratio of the stored energy before and after the slab is inserted if the voltage is kept constant
dividing U1 and U2 which are
U_{1} = \frac{1}{2} \frac{\epsilon_{0} A}{d-b} \Delta V^2
U_{2} = \frac{1}{2} \frac{\epsilon_{0} A}{d} \Delta V^2
\frac{U_{1}}{U_{2}} = \frac{d}{d-b}
Find the work done on the slab as it is inserted. Is it pulled in or pushed in?
Well find the difference in the energy U1 - U2 right?
U_{f} - U_{i} = \epsilon_{0} A (\frac{1}{d-b} - \frac{1}{d}
this change is positive value. So the slab must be pushed in. Is this right?
Please do advise on any mistakes i may have made.
Thank you for your help!

 

[stunner5000pt]

can someone advise me on whether i am right or not on the last part of this problem? I know the first and second parts are correct but what about the last part ? Since the nergy of the system goes up there must be external work done... so the slab mustb e pushed in, yes?

 

[ehild]

can someone advise me on whether i am right or not on the last part of this problem? I know the first and second parts are correct but what about the last part ? Since the nergy of the system goes up there must be external work done... so the slab mustb e pushed in, yes?

Some of the external work is done by the battery or other source that keeps the voltage constant across the capacitor.
As the final capacitance is higher than the initial one and the voltage stays the same, the charge increases. The work done by the battery is the constant voltage multiplied by the increment of charge. The change of energy is the summ of your work and the work done by the battery
\Delta E = \Delta Q U + W
ehild

 

[sammu]

I have the same problem but how do i find the potential difference as a function of x. Also what is the electrostatic energy of the system and force on the dielectric.

 

[maverick280857]

Do you know the electric field in the dielectric and in the free space region? What is the relationship between V and E ?

 

[maverick280857]

Electromagnetic Theory by Reitz is a good book to learn more about dielectric slabs from...