Differences in the Brightness of bulbs for 2 separate circuits

[mhrob24]

Homework Statement

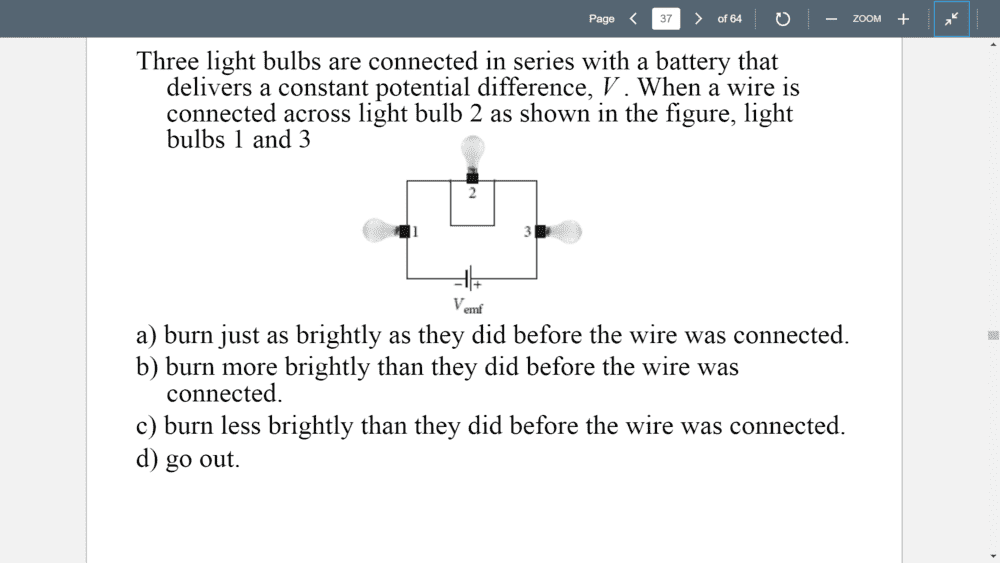
When a wire is connected across bulb 2 as shown, determine what happens to bulbs 1 and 3

Relevant Equations

P = VI
Kirchhoff's rules

I came across 2 similar example problems while studying for my exam and I want to make sure I get the differences between the two before I take my test later this evening. (This might be long but I have an exam coming up and I don't want to go into it with any uncertainties. I appreciate anyone who reads through it and corrects me where I'm wrong in my understanding)

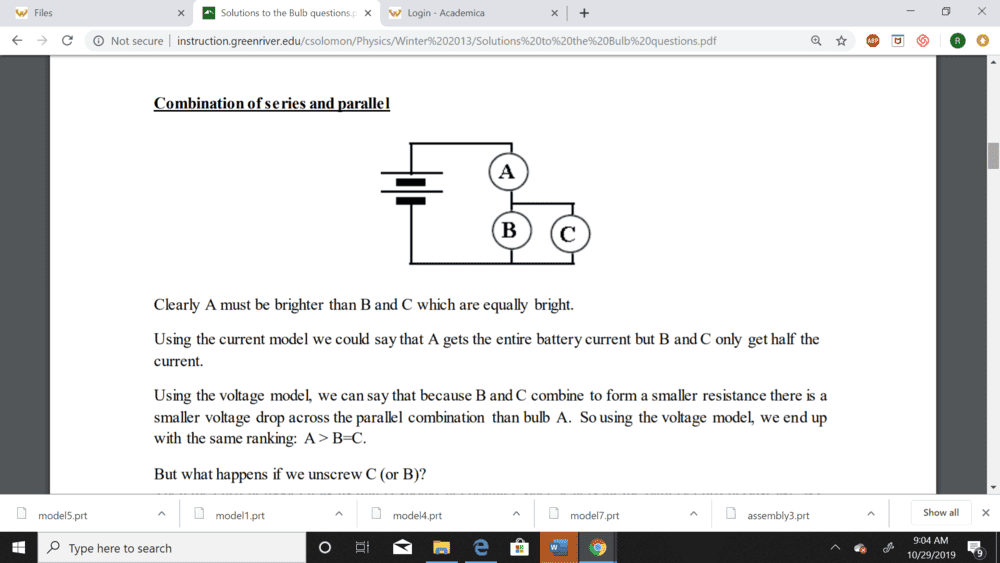
So, the example in the first screenshot I get. Bulb A gets the full current of the batter. After exiting bulb A, the current reaches a node where it splits up, so B and C will be equally bright, but less bright than A because of the reduced current going through them (P = VI). Also, because B and C are in parallel, they combine to a smaller resistance. The equivalent bulb (lets call it bulb BC), will have a lower potential drop across it than bulb A (V = IR, lower resistance means lower voltage, and lower voltage means less power aka brightness). If C is removed, then the remaining bulb B will now have a higher resistance across it now that the resistance from bulb C has been removed. This higher resistance means a lower current running through the circuit ( If B now has a higher resistance with the absence of C, A and B are now in series so the resistances add up, meaning a higher total resistance in the entire circuit). So both B and A will be dimmer than before (with B being brighter than A because of the higher resistance)

The example in the second screenshot is where I'm a little unsure. So let's just pick current to be conventional in this case. So Bulb 3 gets the full current from the circuit. Now with that wire added to the circuit, the current will hit that node and split up. So bulb 2 will NOT get the full current, making it less dim. However, With Kirchhoff's junction rule, the sum of the current flowing out from bulb 2 and out from the added wire will equal the current going into the node. If I'm correct, that means that bulb 1 should get the same current that bulb three got. So bulb 2 should be less dim than 3 and 1, with 3 and 1 being equally bright. However, the answer I was given to this problem by my professor was answer b: bulbs 1 and 3 burn more brightly than they did before the wire was connected. Is that right or am I right? I can't see how bulbs 1 and 3 can be brighter with that wire connected. Its a wire of negligible resistance...?

 

[Antarres]

In the first picture, you got everything right except for unscrewing. Assuming that all three bulbs have the same resistance, once you unscrew bulb B or C, you will get same current and resistance through the remaining bulb, so it will shine as bright as A. Now the total circuit will have higher resistance than before, so both bulbs will be dimmer than before, but they will shine the same(B will not be dimmer than A). That is providing they are all the same bulbs, which I assume is the case.

In the second case, you take into consideration that in circuit exercises unless told otherwise, wires have zero resistance. So when you connect a wire across the bulb 2, all the current will go through that wire since resistance through it is zero. So it will be equivalent to eliminating bulb 2 and replacing it with a wire. In that case, the total circuit resistance will be lower so those two remaining bulb will shine more brightly, as they will get more power. So bulb 1 and 3 will shine equally brightly, but bulb 2 won't shine, and compared to case without the connected wire, bulbs 1 and 3 will shine more brightly than before since they get more power.