Differential Amplifier find currents, and Gain

[DODGEVIPER13]

Homework Statement

For the differential amplifier circuit given above, for all transistors except Q1 and Q2 we have:
β=100, VA=80 V, RC =20 k, VT=0.026 (Thermal voltage), VBE(on)=0.7 V

a-Determine the collector currents IC1, IC2, IC3 and IC6
b-Calculate the Differential mode voltage gain Vo2/Vd.
c-What is the output resistance of the three transistor current source that is biasing the differential pair? Find the numerical value. Does this effect the common mode voltage gain? Explain briefly.
d-calculate the overall Gain

Homework Equations

The Attempt at a Solution

So the first thing I did was find I1 = V-Vbe-V(-)/R1 = 1 mA and Ic3=I1=1 mA then Ic1=Ic2=Ic3/2=0.5 mA and I have V02=V-Ic2(Rc) = 15-0.5(2) = 5 Volts then Ic6 = 15-5-.7/6 =1.55 mA. Next I found differntial mode gain rpi1= Vtβ/Ic = 0.026*100/0.5 = 5.2 kΩ and Rib6= rpi6+(1+β)Re = ?? rpi6= 100*0.026/1.55 = 1.67 mA so Rib6=1.67+(101)(4.3) = 435.97 and gain is β(R||Rib6)/2(rpi1+Rb) = 132.8. For part c Ro= Va/Ic3 = 80/1 = 80 kΩ and yes because if Ro changes so does Av when Av=something/(something)*(Ro). Calculate the overall gain well I would first need to find A2 and A3 and then plug into the formula Ad=Ad1*A2*A3 = ?? However I am unsure of how to proceed what should I do now

 

[DODGEVIPER13]

Ok I uploaded a pdf of my work to make it cleared and I also made an attempt at part d.

 

[DODGEVIPER13]

Hey is there anything I can do to make the question more clear? ? I know I tend to write poorly worded questions, so just let me know if it is too confusing.

 

[rude man]

DodgeV, I think one reason for no-shows is your attempt description is too run-in. Split the sections up into paragraphs would help a lot. On top of that, there's a lot of detail here that I suppose many of us just don't have the time/energy/patience/inclination/whatever to sift thru all your work.

It would be good if you concentrated on one of the parts you're least sure about. We're here to give you hints if you're stuck, not necessarily proofread all your work (if I'm out of line here I'm sure I'll hear about it soon ...).

Anyway, for part (d) the overall gain is the gain from either input to Q2-c and then from that to Q6-c. I would consider Q2-c unloaded but maybe your teach wouldn't agree.

How are you modeling the Early voltage? By a resistor = Va/Ic between emitter and collector?

 

[DODGEVIPER13]

Ok man yah you are probably right well I found my error on part (a) but I am stuck on the differentail mode gain I had one of my friends assist me Adm = -gmRC/2 = -IC1RC/2VT = -(0.5)(20)/2(.026) = -192.3075 is that ok?

 

[rude man]

Ok man yah you are probably right well I found my error on part (a) but I am stuck on the differentail mode gain I had one of my friends assist me Adm = -gmRC/2 = -IC1RC/2VT = -(0.5)(20)/2(.026) = -192.3075 is that ok?

Do you define the differential gain as Vo2/(v1-v2)? If so, why the 'divide by 2'? You're already figuring the Q2 current as 0.5 mA.

You're ignoring the 2K base resistors but frankly I would too.

 

[DODGEVIPER13]

Ok so in your opinion which looks better because I got that equation -Ic1RC/2VT from a friend and I am defining it as Vo2/Vd. Honestly as far as dividing by 2 I am not sure what does the division by 2 mean? I get lost on the gain stuff I can handle the DC analysis.
This is my equation:
Beta(R||Rib6)/2(rpi1+RB)

 

[rude man]

Ok so in your opinion which looks better because I got that equation -Ic1RC/2VT from a friend and I am defining it as Vo2/Vd. Honestly as far as dividing by 2 I am not sure what does the division by 2 mean? I get lost on the gain stuff I can handle the DC analysis.
This is my equation:
Beta(R||Rib6)/2(rpi1+RB)

The differential gain IS a dc computation.
I don't see any Vd on the schematic. I guess Vd = v1 - v2?
You "equation" is the differential gain? I don't think so. What is Rib6? What is R? Try to stick to symbols on the schematic where possible. You were a lot closer before. I don't have time right now but I think I goofed and I believe the divide by 2 is correct. Right now looks like the differential gain is indeed I_C1*R_C/2V_T but i want to double-check.
More later.

 

[Jony130]

Because we have 2K resistors at differential pair input the voltage gain will not be equal to RC/2re = IC1*RC/2VT = 192.
The gain will drop to

\Large Av = \frac{Rc}{2re + \frac{2*2K}{\beta+1}} = 139V/V

And if we include Early voltage rce ≈ 80V/500μA = 160kΩ and Q6 input impedance we have

rce = 160kΩ and RinQ6 ≈ (β + 1)*5.3kΩ = 535kΩ. The gain will drop to

Av =\Large \frac{Rc||rce||RinQ6}{2re + \frac{2*2K}{\beta+1}} = 120V/V

 

[The Electrician]

Q

Hi, Jony130,

I noticed that in post #1, the OP gives us:

"For the differential amplifier circuit given above, for all transistors except Q1 and Q2 we have: β=100, VA=80 V, RC =20 k, VT=0.026 (Thermal voltage), VBE(on)=0.7 V"

You have done what I would, which is to assume that Q1 and Q2 have the same specs, but I wonder why the problem excepted Q1 and Q2? Does the problem want the student to use some other parameters for them?

 

[DODGEVIPER13]

Hmmm just read that I think it means they have different parameters. would that affect Ic1 and 2 I guess not because I never used parameters to find them. On another note if I where to try to find the gain like jony how would I do that

 

[DODGEVIPER13]

Also I am in an area where I can't really give you Rib6 or the other values requested but I will later on

 

[The Electrician]

Hmmm just read that I think it means they have different parameters. would that affect Ic1 and 2 I guess not because I never used parameters to find them. On another note if I where to try to find the gain like jony how would I do that

It won't affect Ic1 and Ic2, but if the Early voltage and β is different for Q1 and Q2, the gain will be affected.

 

[DODGEVIPER13]

ok so how would I go about starting to find gain? I mean I know what I see in the book and what my buddies show me but I really don't get it.

 

[DODGEVIPER13]

Rib6=rpi6+(1+beta)Re rpi6=beta*Vt/Ic6 rpi1=beta*Vt/Ic1 and Rc= 20 k

 

[The Electrician]

Rib6=rpi6+(1+beta)Re rpi6=beta*Vt/Ic6 rpi1=beta*Vt/Ic1 and Rc= 20 k

It would make it easier for those of us who are helping you if you wouldn't put everything on one line; it's hard to read. Do it like this instead:

Rib6=rpi6+(1+beta)Re
rpi6=beta*Vt/Ic6
rpi1=beta*Vt/Ic1
Rc= 20 k

To get the voltage gain of the differential pair you have take into account that the load on Q1 and Q2 is not just Rc.

The Early effect creates an apparent resistance (sometimes denoted "ro"; Jony130 called it rce) from collector to emitter of a transistor. The ro for Q1 and Q2 is 160000 ohms; you have to include that in the load on Q2, as well as Rpi6.

Look at what Jony130 did in post #9. That should give you some guidance.

 

[DODGEVIPER13]

Ok, I am starting to get it. Where exactly is rpi located? I now know ro is over the collector to emitter. Also would it help for me to draw the small-signal equivalent? Furthermore what is K and re is his formulation I assume re means Re which is 5.3 K

 

[The Electrician]

Ok, I am starting to get it. Where exactly is rpi located? I now know ro is over the collector to emitter. Also would it help for me to draw the small-signal equivalent? Furthermore what is K and re is his formulation I assume re means Re which is 5.3 K

Where is rpi located? I guess you could say that it's inside the transistor, just like ro and re are. Yes, it might help to draw the small-signal model, because then Rpi, ro and re will be shown explicitly.

K means 1000. Where Jony130 has 2*2K, that means 4000 ohms.

re means the internal emitter resistance, given by .026/Ic for each transistor.

Your schematic shows a resistor R_E of 5300 ohms connected from the emitter of Q6 to ground; that's not the same as Re.

 

[Jony130]

Hi, I prefer to use T small-signal model.
And re - is small signal resistance between base and emitter looking into the emitter with base short to ground.

re = Vt/Ie ≈ Vt/Ic ≈ 1/gm

but you prefer to use hybrid-pi model so Rpi = (β + 1)*re

http://www.ittc.ku.edu/~jstiles/412...Models/The Hybrid Pi and T Models lecture.pdf
https://www.physicsforums.com/showpost.php?p=4513521&postcount=30

 

[DODGEVIPER13]

I get how to do small-signal equivalents for single transistor circuits, but multistage circuits are giving me problems. Are there any example multistages, that break it doen step by step? I have uploaded my first attempt.

 

[The Electrician]

That's a start, but you have a few problems.

The emitter of Q6 is not connected to the emitters of Q1 and Q2. The emitter of Q6 goes to ground through a resistor, RE.

The emitters of Q1 and Q2 are connected together, but then they go to ground through the collector of Q3. I wouldn't bother showing Q3 as a model; just replace it with an 80k resistor to ground (for small signal purposes that's its equivalent; it's really the ro of Q3).

Q6 has a different emitter current than Q1 and Q2 (I think you calculated something like 1.55 mA), so its r∏ and ro are different. I called them r∏6 and ro6.

Once you get all this right, then you will have to write some nodal equations for the whole thing.

This is actually a fairly complicated problem if you include all the various items such as ro and r∏ for all the transistors, different values for load resistors and RE6, etc.

 

[DODGEVIPER13]

Ok so is my second attempt improved over my first?

 

[The Electrician]

The top end of ro6 should not be connected to the r∏ just to its left.

The bottom end of ro6 should not go to ground, but to the emitter of Q6.

The end of Rc6 that you have grounded should go to V+ just for consistency, even though V+ is also AC ground.

The bottom end of r∏6 should go to the emitter of Q6, not to ground.

The top ends of all your r∏ resistor should NOT be connected to the top of the gm sources.

The collector of Q2 (the top end of its gm source) should go to the top end or r∏6.

The top end of Rc6 and the top end of r∏6 should not be connected.

Check out the layout and connections of the Q6 model.

 

[DODGEVIPER13]

Ok the rpi appears to be tripping me up so it is the resistance between the base and emitter correct? If that is so then I probably still have mistakes however I feel that this is improved on my 3rd attempt

 

[The Electrician]

You've still got the emitter of Q6 connected to the emitters of Q1 and Q2. Remove that connection and add an 80k ohm resistor from the emitters of Q1 and Q2 to ground.

You should probably give the two rpi resistors associated with Q1 and Q2 different names. Let rpi1 be the Q1 resistor, and rpi2 the Q2 resistor. Then the gm sources need to be also particularized to the appropriate transistor. You'll need to be sure that the voltage applied to the base of Q1 controls the collector current of Q1, the Q2 base voltage controls Q2 collector current, the Q6 base voltage controls the Q6 collector current, etc.

 

[DODGEVIPER13]

Ok man here is my 3rd revision when I get this right I will attempt the KVL.

 

[DODGEVIPER13]

Actually being that I have never attempted a small signal of a circuit this big how would I do the KVL using different GM values?

 

[The Electrician]

The last problem I see is ro6. Disconnect the bottom end of ro6 from the emtters of Q1 and Q2, and connect it to the emitter of Q6.

I would recommend a nodal solution for this problem. This means using KCL to set up your nodal equations.

Set your equations in symbolic form first. Use different gm values where needed. I think gm1 and gm2 are the same, but gm6 will be different.

 

[DODGEVIPER13]

I changed my circuit and drew the currents I also did a KCL on the node of the 80 K resistor and at the node above Re I probably did it wrong but here is my attempt.

 

[The Electrician]

Your circuit looks ok, but you've made a mistake in your calculation of gm for the transistors. gm is Ic/Vt, not Ic/Vbe.

Now to solve the network using the nodal method, you need to select a reference node (use ground in this case. V+ and V- are at signal ground also; don't forget this when setting up your equations).

Something I highly recommend is to use red ink and label all your nodes (excluding the reference node). I'd label the nodes with lower case v and node numbers like this: v1, v2, v3, etc. Leave the input voltages V1 and V2 with upper case V. You have 7 nodes to solve:

v1. Top of V1
v2. Top of ro1
v3. Top of 80k resistor
v4. Top of ro2
v5. Top of V2
v6. Emitter of Q6
v7. Collector of Q6 (your output node)

This will give you 7 nodal equations. You'll want to use some kind of linear equation solver to solve them.

Write your equations using symbolic variables to start. Once you have them correct, then you can substitute numeric values and actually get node voltages. Don't try to solve the equations with the symbolic variables; it would get completely out of hand.

For example your first equation could be:

\frac{v1-v2}{RB+rpi1}=Ib1

That leaves 6 more equations, and they will be more complicated.

Edit: Did you ever find out why the problem says:

"For the differential amplifier circuit given above, for all transistors except Q1 and Q2 we have:
β=100, VA=80 V, RC =20 k, VT=0.026 (Thermal voltage), VBE(on)=0.7 V
"

Maybe they don't expect you to include the effect of ro with respect to Q1 and Q2, (and possibly Q6?). Doing so does complicate the solution.

 

[DODGEVIPER13]

As far as that goes I am still unsure I like Jonys gain though it matches up with what the professor said the numerical value of the gain should be. As for the rest I will do this later.

 

[DODGEVIPER13]

Ok so I am going to put it on here and I am going to upload it later tonight. Ib1=V1-V2/Rb+rpi1, Ib2=V5-V4/Rb+rpi2, Ie1 = V2-V3/ro1, Ie1+Ie2=Ic3, Ie2 = V4-V3/ro2, gm6Vbe6 = V7-V6/ro6

 

[The Electrician]

If you don't use lower case v plus the node number (v1, v2, etc.) like I suggested, it won't be possible to distinguish between the input voltage sources V1 and V2, and nodes v1 and v2.

What you're going to get by doing all this is a full solution to the network without approximation. Is this what your friends are doing, or are they using approximate methods?

Jony130 gave a result that is quite close to the answer obtained with the 7 node formulation. Would that be good enough?

 

[DODGEVIPER13]

Yes I guess so man I don't think my buddies really get this problem either they are just pulling formulas from the book I think I would be better off letting this part go and just going with what Jony and you provided. That being said how would I start on part d ultimatley that was where I was trying to get the total gain?

 

[DODGEVIPER13]

I think my friends were using approximate methods to obtain gain.

 

[The Electrician]

Ok so I am going to put it on here and I am going to upload it later tonight. Ib1=V1-V2/Rb+rpi1, Ib2=V5-V4/Rb+rpi2, Ie1 = V2-V3/ro1, Ie1+Ie2=Ic3, Ie2 = V4-V3/ro2, gm6Vbe6 = V7-V6/ro6

You need to be very careful with your equations. When you type them in text form as you have done here, you need to use parentheses where there could be ambiguity. For example, you have typed:

Ib1=V1-V2/Rb+rpi1, which is the same as:

Ib1 =V1 - \frac{V2}{Rb}+ rpi1

which is not what you really want. What you really want is:

Ib1 =\frac{V1-V2}{Rb+ rpi1}

In plain text form you would need to use some parentheses to get a correct representation, like this:

Ib1=(V1-V2)/(Rb+rpi1)

Don't use this for equation 1; I'm going to change the nodes below.

You can use LaTeX on this forum to get the pretty expressions as I've done above. Here's an FAQ that explains how to do it:

https://www.physicsforums.com/showpost.php?p=3977517&postcount=3

Yes I guess so man I don't think my buddies really get this problem either they are just pulling formulas from the book I think I would be better off letting this part go and just going with what Jony and you provided. That being said how would I start on part d ultimatley that was where I was trying to get the total gain?

Parts b and d can both be answered by using the model you have so far. You only need to set up the 7 nodal equations and solve them. Sounds easy, right?

Please use lower case v for the node designators; for small signal analysis, lower case letters are conventionally used for variables.

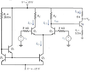
We will get easier results if two of the nodes are changed slightly. Let's use these node designators:

v1. Top of rpi1
v2. Top of ro1
v3. Top of 80k resistor
v4. Top of ro2
v5. Top of rpi2
v6. Emitter of Q6
v7. Collector of Q6 (your output node)

This will change your equation 1. Here's how we derive it.

The voltage at each node is given by the relevant designator; at node 2, the voltage is v2. Currents leaving a node are considered positive and those entering a node are negative.

There are two paths for current at node 1: the input current in RB1 and the current in rpi1.

1. The current in RB1 is just the voltage across RB1, which is (v1-V1), divided by the resistance RB1: (v1-V1)/RB1. (Here's why you need to use lower case v for the node voltages. v1 is the voltage at the top of rpi1 and V1 is the input voltage). This current is leaving node 1 because we chose to define the voltage as (v1-V1), not (V1-v1); see the explanation at the end of this post for more info about this.

2. The current in rpi1 is the voltage across rpi1, which is (v1-v3), divided by the value of rpi1: (v1-v3)/rpi1

Equation 1 simply sets the sum of these two currents equal to zero:

Eq1: (v1-V1)/RB1 + (v1-v3)/rpi1 = 0



Let's derive equation 2.

We have 3 currents leaving node 2 (If any are actually entering, the algebra will give a negative sign for them; that is taken care of by the order of the subtraction of voltages in the numerator expression for each current).

1. The current in the collector resistor of Q1 (which you should have labeled Rc1, not just Rc) is equal to the voltage across it, which is (v2-0), (remember that V+ is signal ground) divided by the resistance itself: (v2-0)/Rc1 which is just v2/Rc1. That is a current leaving node 2.

2. The current in the resistor ro1 is the voltage across ro1, which is (v2-v3), divided by the resistance of ro1: (v2-v3)/ro1

3. The current supplied by the gm1 source; that current is gm1*vbe1. But, notice that Vbe1 is just (v1-v3), so this current is given by gm1*(v1-v3)

Equation 2 is just the sum of these 3 currents set equal to zero:

Eq2. v2/Rc1 + (v2-v3)/ro1 + gm1*(v1-v3) = 0

You should be able to see how this works. You identify all the paths for current to leave or enter a node; those paths are often just some impedance, although they are sometimes sources such as the gm sources. If the path is an impedance, write an expression for the numerator of a fraction, that expression being the voltage across the impedance in a form like this (va-vb). The va is the voltage at the node being worked on, and vb is the voltage at the other end of the impedance; by ordering the voltages like this: (va-vb) instead of (vb-va) the current is calculated as if leaving the node and is therefore a positive current. The denominator is just the impedance under consideration.

If the path is a controlled source such as your gm sources, write an expression for the current supplied by the source, involving the voltage(s) at some other nodes, where those nodes are the ones whose voltages control the source.

Each current is in the form of a fraction (except possibly for the currents from controlled sources) and all the currents are summed to zero to give you an equation.

Derive the next 5 equations and post them, each on a separate line, not all on one line separated by commas!

You will need to solve 7 simultaneous equations; how will you do that? Do you have access to Matlab, MathCad, or some similar software?

 

[DODGEVIPER13]

\frac{v1-V1}{R_B1} + \frac{v1-v3}{r_pi1}=0

\frac{v2-0}{R_c1} + \frac{v2-v3}{r_o1} + gm1*(v1-v3)=0

gm1*(v1-v3) + gm2*(v5-v3) + \frac{v3}{80}=0

\frac{v4}{R_c2} + \frac{v4-v3}{r_o2} + gm2*(v5-v3)=0

\frac{v5-V2}{R_B2} + \frac{v5-v3}{r_pi2}=0

gm6*(v7-v6) + \frac{v4-v6}{r_pi6} + \frac{v6-v7}{r_o6} + \frac{v6}{R_E}=0

\frac{v7-v6}{r_o6} + \frac{0-v7}{r_c6} + gm6*(v7-v6)=0

 

[DODGEVIPER13]

Well I tried LAtex and I don't think it worked but on line 3. Well anyways if you can see it then I believe I may have made mistakes in 6 or 7?

 

[The Electrician]

\frac{v1-V1}{R_B1} + \frac{v1-v3}{r_pi1}=0

\frac{v2-0}{R_c1} + \frac{v2-v3}{r_o1} + gm1*(v1-v3)=0

gm1*(v1-v3) + gm2*(v5-v3) + \frac{v3}{80}=0

\frac{v4}{R_c2} + \frac{v4-v3}{r_o2} + gm2*(v5-v3)=0

\frac{v5-V2}{R_B2} + \frac{v5-v3}{r_pi2}=0

gm6*(v7-v6) + \frac{v4-v6}{r_pi6} + \frac{v6-v7}{r_o6} + \frac{v6}{R_E}=0

\frac{v7-v6}{r_o6} + \frac{0-v7}{r_c6} + gm6*(v7-v6)=0

OK, let me see if I can figure out what's wrong with LaTex. Well, I didn't do anything and it works for me.

You have a few errors:

EQ1. \frac{v1-V1}{RB1} + \frac{v1-v3}{rpi1}=0

EQ2. \frac{v2-0}{Rc1} + \frac{v2-v3}{ro1} + gm1*(v1-v3)=0

In EQ3, the gm sources should have a minus sign because their current flows
INTO node 3, but out of nodes 2 and 4. The resistor from node 3 to
ground should be 80,000 not 80.
EQ3. -gm1∗(v1−v3)-gm2∗(v5−v3)+\frac{v3}{80000}=0

In EQ4, you forgot the current leaving that node into rpi6.
EQ4. \frac{v4}{Rc2} + \frac{v4-v3}{ro2}+\frac{v4-v6}{rpi6} + gm2*(v5-v3)=0

EQ5. \frac{v5-V2}{RB2} + \frac{v5-v3}{rpi2}=0

In EQ6, gm6 is negative and the voltage controlling it is (v4-v6). The term (v4-v6)/rpi6 should
be reversed; remember the first variable in the numerator corresponds to the node you're working on (but not for the gm source).
EQ6. -gm6*(v4-v6) + \frac{v6-v4}{rpi6} + \frac{v6-v7}{ro6} + \frac{v6}{RE}=0

In EQ7, the (0-v7) term should be reversed. The controlling voltage for gm6 is (v4-v6), not
(v7-v6). Use capital R for Rc6.
EQ7. \frac{v7-v6}{ro6} + \frac{v7-0}{Rc6} + gm6*(v4-v6)=0


You're in the home stretch now. Substitute numeric values for all your parameters and solve the 7 equations.

Here are the values I used:

We want the differential gain, so set V1 to 1/2 and V2 to -1/2; that way the applied differential voltage is 1 volt, and the voltage at node 4 will be the gain you need for part b of your problem. The voltage at node 7, v7, is the gain you need for part d.

Post your results so I can check for errors.

 

[DODGEVIPER13]

Ha well I started doing this by hand it is a nightmare I so far have V2=898.364V1-790.88
V3=2.627V1-1.313
V1=0.6172+0.2349V5

Maybe I should use Matlab but how would I even do that I entered al the variables in but since v1 would be undefined that would confuse me?

 

[DODGEVIPER13]

Oh wait I would need to set up individual functions wouldn't I

 

[The Electrician]

v1,v2,v3,v4,v5,v6,v7 are all unknowns. They are the voltages which exist at the 7 nodes.

There's no way you will be able to solve 7 simultaneous equations by hand without making mistakes (unless you have a great deal of experience doing so)!

Using "solving multiple equations in Matlab", I get a lot of hits, such as:

http://www.ehow.com/how_8718288_solve-simultaneous-equations-using-matlab.html

http://www.mathworks.com/help/symbolic/solve.html

 

[The Electrician]

Don't fail to set all your parameters to their numeric values before you try to execute a multiple equations solver. Do it by including some assignment statements like this before running the solver:

 

[The Electrician]

Just to help you know when you've got it right, I'll tell you the first two voltages:

v1=.362107
v2=-122.569

 

[DODGEVIPER13]

ugggg MATLAB says Undefined function or method 'solve for input arguments of type char

>> V1=0.5;
>> V2=-0.5;
>> RB1=2000;
>> RB2=2000;
>> Rc1=20000;
>> Rc2=20000;
>> gm1=.01904;
>> gm2=gm1;
>> gm6=.0308957;
>> ro1=160000;
>> ro2=160000;
>> rpi1=5252;
>> rpi2=5252;
>> ro6=98605;
>> rpi6=3236.7;
>> RE=5300;
>> Rc6=6000;
>> [v1,v2,v3,v4,v5,v6,v7]=solve('((v1-V1)/(RB1))+((v1-v3)/(rpi1))=0','((v2)/(Rc1))+((v2-v3)/(ro1))+gm1*(v1-v3)=0','-gm1*(v1-v3)-gm2*(v5-v3)+((v3)/(80000)) = 0','(((v4)/(Rc2))+((v4-v3)/(ro2))+((v4-v6)/(rpi6))+gm2*(v5-v3)=0','((v5-V2)/(RB2))+((v5-v3)/(rpi2))=0','-gm6*(v4-v6)+((v6-v4)/(rpi6))+((v6-v7)/(ro6))+((v6)/(RE))=0','((v7-v6)/(ro6))+((v7)/(Rc6))+gm6*(v4-v6)=0')

 

[DODGEVIPER13]

hmmmm it seems solve is undefined in my version of MATLAB it seems will wolfram work?

 

[The Electrician]

A quick look at your Matlab solve statement reveals, for example, unbalanced parentheses in equation 4:

(((v4)/(Rc2))+((v4-v3)/(ro2))+((v4-v6)/(rpi6))+gm2*(v5-v3)=0

You've got parentheses in there you don't need. You could write it like this:

(v4)/(Rc2)+(v4-v3)/(ro2)+(v4-v6)/(rpi6)+gm2*(v5-v3)=0

There may be more, but look over everything VERY carefully. That sort of thing is probably your problem.

 

[The Electrician]

hmmmm it seems solve is undefined in my version of MATLAB it seems will wolfram work?

If you fix the problem I mentioned above and it still won't work (which I don't see why it shouldn't), then you could try another program.

Is Matlab something you found on your school's network?

What do you mean by Wolfram? There is a program called Mathematica made by Wolfram; it might be on your school's network. Then there's Wolfram Alpha, which is a web resource.

 

[DODGEVIPER13]

yah man I just tried it oh well no worries I will have to just go with what I got the test is tomorrow and its late.

 

[DODGEVIPER13]

Hey man thanks to you and all who helped. The way you explained it really helped me understand and I would have had it if I wouldn't have run into issues with matlab.