Nilupa
- 18
- 0
Can anyone help me on this equation. I want to find a solution for dr/dt. a, b and c are constants.
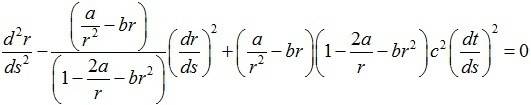
Last edited:
HallsofIvy said:In general, you can't solve a single equation for multiple unknowns. And here you have, even counting a, b, and c as given constants, two unknown functons, r and s, in one equation.
(This is NOT a "partial differential equation"- there is only one independent variable, t.)
Nilupa;3995763 I want to find a solution for dr/dt[/QUOTE said:I believe you can solve for \frac{dr}{dt} in that. Note that:
\frac{dr}{ds}=\frac{\frac{dr}{dt}}{\frac{ds}{dt}}
Ok then, just turn the crank now.
jackmell said:I believe you can solve for \frac{dr}{dt} in that. Note that:
\frac{dr}{ds}=\frac{\frac{dr}{dt}}{\frac{ds}{dt}}
Ok then, just turn the crank now.