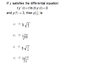Northbysouth
- 241
- 2
Homework Statement
If y satisfies the differential equation:
ty'(t) + tln(t)y(t) = 0
and y(1) = 3 then y(1/2) = ?
I have attached an image of the question with the possible solutions:
Homework Equations
The Attempt at a Solution
Initially I tried plugging in t=1 and y(1) = 3 giving me:
y'(1)+3ln(1) = 0
Hence y'(1) = 0
I did the same for t=1/2
1/2[y'(1/2) + ln(1/2)y(1/2)] = 0
But this doesn't seem to help me. Any suggestions would be appreciated.