- #1
opus
Gold Member
- 717
- 131
Homework Statement
A spherical balloon is being filled with air at a constant rate of ##2cm^3/sec##.
How fast is the radius increasing when the radius is 3 cm?
Homework Equations
The Attempt at a Solution
This is a problem given and spelled out in my text. However, it seems to be assuming that the reader knows what to do with the units and that is unfortunately not the case with me.
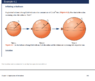
If you'll have a look at the posted image, I have highlighted where units have been added into the RHS of the equation. I understand the substitution on the LHS, but I have a couple of questions in regard to the RHS.
First, we had an original volume function written as ##V(t) = \frac{4}{3}π[r(t)]^3cm^3## and we differentiated both sides, giving ## \frac{dV}{dt} = 4π[r(t)]^2\frac{dr}{dt} ## Notice that the cm units are missing. Why were they taken out?
Second, after we made the substitution (the line which is highlighted in the image), we brought two separate units back in- one was ##cm^2## and one was ##\frac{cm}{s}##.
Thirdly, after we solved for ##\frac{dr}{dt}##, the units didn't cancel out, even though we had a ##cm^3## and ##sec## in both the numerator and the denominator.
Thank you for any help you can provide.