ashah99
- 55
- 2
- Homework Statement
- Please see a snippet of the problem below.
- Relevant Equations
- C/N = (Eb/N0) * (data rate/bandwidth)
Problem Statement:
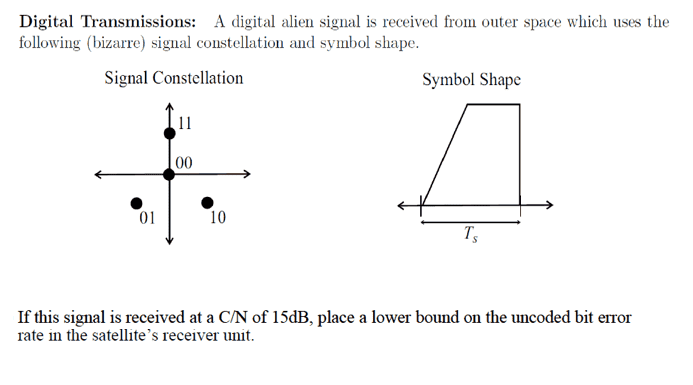
I am not quite sure how to approach this problem and would appreciate the help. I how the C/N is closely related to the SNR (Eb/N0), but the question does not give the bandwidth or data rate for me to use the formula above. From the constellation diagram, my guess is this is QPSK modulation scheme, but even that is a guess. Can anyone help?
I am not quite sure how to approach this problem and would appreciate the help. I how the C/N is closely related to the SNR (Eb/N0), but the question does not give the bandwidth or data rate for me to use the formula above. From the constellation diagram, my guess is this is QPSK modulation scheme, but even that is a guess. Can anyone help?