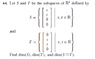pyroknife
- 611
- 4
I've attached the problem.
For S:
I form the matrix:
1 0
0 1
0 0
0 0
Thus the dimension is 2.
For T:
I form the matrix
0 0
1 0
0 1
0 0
Thus the dimension is also 2.
Is that the correct idea?
Also what does S ∩ T mean? I couldn't find the symbol in my textbook.
For S:
I form the matrix:
1 0
0 1
0 0
0 0
Thus the dimension is 2.
For T:
I form the matrix
0 0
1 0
0 1
0 0
Thus the dimension is also 2.
Is that the correct idea?
Also what does S ∩ T mean? I couldn't find the symbol in my textbook.