Dipole EM wave field lines VS decreasing amplitude

[DoobleD]

The E and B field lines of a dipole radiating EM waves looks like that (sorry for the poor quality) :

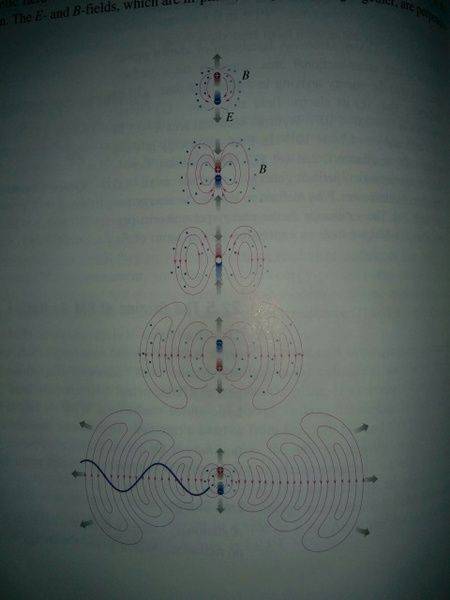
What I wonder is how can we see that the amplitude of the fields decrease as 1 / r? When you look as such a picture it actually feels likes the amplitude should rises. The E field gets "elongated".

But I know that the radiated energy is spread over a growing sphere/torus like shape, thus the fields amplitude must weaken over time and distance.

I don't understand how the fields weakens when I look at those EM radiation drawings.

 

[DoobleD]

Also I don't see how to make the link between the picture of a radiating dipole, like the one above, and the picture of a plane EM wave. What's even more confusing is that :

1 - if the radiation sphere is huge, you can approximate the radiation at a point as a plane wave radiation.
2 - BUT plane wave radiations don't decrease in energy. Their field amplitude maximum stays the same.
3 - So what? Is the decrease too small to be taken in account when we are close to a huge radiation sphere?

 

[jtbell]

Individual field lines show only the direction of the field at points on the lines.

If the field lines are drawn "properly", their spacing (separation) in a region should correspond roughly, in an indirect way, with the magnitude of the field in that region. Larger spacing would mean smaller magnitude (weaker field). It doesn't appear that your book's diagrams have been drawn carefully enough to show that.

The animation on this Wikipedia page is a bit better:

https://en.wikipedia.org/wiki/Antenna_(radio)

It shows the maxima and minima of the field within a few wavelengths of the source. It's not big enough to show how the amplitude of the maxima decrease as 1/r as you get further and further away from the source. For that, I think you need a diagram that is many wavelengths wide so as to get away from the near-field region.

 

[jtbell]

1 - if the radiation sphere is huge, you can approximate the radiation at a point as a plane wave radiation.
2 - BUT plane wave radiations don't decrease in energy. Their field amplitude maximum stays the same.
3 - So what? Is the decrease too small to be taken in account when we are close to a huge radiation sphere?

Correct. If you're 10000 meters away from a radio transmitter, and compare the field amplitude at 10000 m with the amplitude at 9999 m, the difference is going to be only about 0.01%.

 

[DoobleD]

Neat answers, thanks!

If the field lines spacing increases, how does the wavelength keeps constant?

BTW while reading your answer I realized I had completely forgot that field strength is represented through line density...

Hm, in EM plane wave drawings like the one below, the field strength there is shown by the vectors magnitude right? Just to be sure I'm not misreading the drawings. It's a little confusing.

 

[jtbell]

If the field lines spacing increases, how does the wavelength keeps constant?

The wavelength is the distance between the places where the field lines are "bunched up" closest together, or the distance between the places where the field lines are "spread out" the furthest from each other; not the distance between the individual field lines. The animation on the Wikipedia page shows about one and a half wavelengths from the antenna in either direction.

in EM plane wave drawings like the one below, the field strength there is shown by the vectors magnitude right?

Right. If you were to draw field lines on top of that, they would run vertically and bunch together at the z-positions where the field strength is a maximum in either direction (the upwards and downwards peaks).

 

[DoobleD]

Thank you.

The wavelength is the distance between the places where the field lines are "bunched up" closest together, or the distance between the places where the field lines are "spread out" the furthest from each other; not the distance between the individual field lines.

Yes, but if the overall magnitude of the fields decreases as 1 / r, then all the lines must be further and further from each other with increasing distance. Both the places where they are more compact (high magnitude) and where they are more spread (low magnitude) must overall be more spread. And still that doesn't affect the wavelength, why?

It's hard to picture, I'll see if I can find some drawing.

 

[jtbell]

Within successive regions in which the field lines are spaced closely together, the lines become further apart (the maximum field strength becomes weaker). But those regions maintain the same distance from each other (the wavelength remains the same).

 

[DoobleD]

Within successive regions in which the field lines are spaced closely together, the lines become further apart (the maximum field strength becomes weaker). But those regions maintain the same distance from each other (the wavelength remains the same).

Ok, I think I finally get it.

I was going to ask how can the lines become further apart because all of space is already "full" of lines. But it is the principle of field lines to assume that some regions have higher densities of lines and some lower densities. Hence, a region with a high density can always spread out, so that the surroundings local densities goes a little up everywhere and the overall region density gets lower. Or more simply, the same quantity of lines take up more space.

What I find confusing with field lines is that it's a kind of drawing with which you can "zoom" in or out as much as you want, and the space is still full of lines everywhere no matter the zoom level. But still, we define some places with higher densities than others. I think this confuses me sometimes.

So here the "compact" regions spread out synchronously into the less compact ones, until everything is smooth, same density all over, which means 0 amplitude. At infinity, I guess.

Anyway, thank you jtbell!

 

[Dale]

These are just illustrations. You seem to think that all such illustrations must conform precisely to some exact standard with precise interpretations.

Illustrations are just pictures intended to convey some point, which is described in the figure caption and text. If you really want to learn it you must understand the math behind the illustration. There is no one size fits all explanation for these figures.

 

[DoobleD]

These are just illustrations. You seem to think that all such illustrations must conform precisely to some exact standard with precise interpretations.

Illustrations are just pictures intended to convey some point, which is described in the figure caption and text. If you really want to learn it you must understand the math behind the illustration. There is no one size fits all explanation for these figures.

I realize those illustrations can't be quantitatively precise, but I expect them to be accurate at least qualitatively. Otherwise they would be useless, I think. While they have not as much value as the equations, it is important to me to understand them, because they usually help me to get a feeling with the equations. And after all, they are just another tool to understand the physics.

That said, it seems wise indeed to not give them too much credit in the sense that they are NOT a picture of reality, which cannot be "draw" but is only described accurately (up to a certain point I guess) by the maths. At least that's how I understand your answer. :D Thank you for the advice, I should keep that in mind.If I may ask one last thing regarding illustrations : in a dipole radiation such as the one pictured here (description here), is there a way to intuitively interpret why/how the E field lines detach from the dipole? The lines of the radiation appear to slowly "close" themselves, one by one, becoming thus independent from the dipole. In what I believe is labelled as the "induction zone" (the other two zones being the "radiation zone" and the "quasi static zone")?

Is there an intuitive way of understanding it, or are we solely limited to saying "well, when you run a software with the equations, it looks like that"?

 

[jtbell]

In an electrostatic situation (not time-varying), the electric field is associated with electric charges, and field lines always start and end on a charge. In an electrodynamic situation (a time-varying one such as an oscillating dipole), the electric field is associated with both electric charges and with time-varying magnetic fields (via Faraday's Law). The fields associated with time-varying magnetic fields tend to form loops, and do not "originate" on charges. The two kinds of electric fields superpose (add together) to produce a single field whose field lines have "mixed" characteristics: sometimes they originate on charges, and then they "break off".

I'd like to emphasize along with DaleSpam that field lines are just a visualization tool. It's possible to define them more or less rigorously in terms of electric flux: the number of field lines passing through a surface is proportional to the electric flux through the surface, if the lines are drawn properly and rigorously. However, the number of field lines per unit of electric flux is arbitrary, so long as it's the same everywhere at a given moment, and you know what the proportionality constant is. (And many (probably most) field-line diagrams at the introductory level are not drawn rigorously according to this prescription.)

As an analogy, consider an x-y position graph drawn on a computer screen, using software that displays one gridline per cm initially. As you zoom in on the graph, the gridlines spread apart, and at some point the software may decide to switch from one gridline per cm to one gridline per mm. There are now ten times as many gridlines, but nothing has really changed about the graph, right? Same thing with field lines. As you "zoom in" on an electric field map, you're free to "change the scale" i.e. change the proportionality between number of field lines and electric flux, so as to "fill in" more field lines between the old ones, so long as you're aware of the new "scale." Nothing changes about the physics in this process.

(Have you studied electric flux and its mathematical definition yet?)

 

[vanhees71]

I don't like this picture of saying the "electric field is associated with time-varying magnetic fields". It's quite misleading an interpretation of Faraday's Law,
$$\vec{\nabla} \times \vec{E}+\frac{1}{c} \partial_t \vec{B}=0.$$
Together with the magnetic Gauß's Law,
$$\vec{\nabla} \cdot \vec{B}=0,$$
it makes up the two inhomogeneous Maxwell equations. They are four constraints on the electromagnetic fields, which is represented by two three-vectors in this (1+3)-dimensional representation of the electromagnetic field.

The two inhomogeneous Maxwell equations, i.e., the Ampere-Maxwell Law and Gauss's Law for the electric field,
$$\vec{\nabla} \times \vec{B} - \frac{1}{c} \partial_t \vec{E}=\frac{1}{c} \vec{j}, \quad \vec{\nabla} \cdot \vec{E}=\rho,$$
describe the source terms, clearly identifying current- and charge-density distributions as the sources of the electromagnetic field. This is also made explicit by the retarded solutions, the socalled Jefimenko equations.

Of course, you can rewrite these solutions such that, e.g., the time-varying magnetic field is treated as a source of the electric field by solving for $\vec{E}$ using only Faraday's Law and substituting this solution into the Ampere-Maxwell Law to solve for $\vec{B}$. But as you'll see, this is a tremendously more complicated picture of the electromagnetic processes, because $\vec{B}$ appears to be a nonlocal functional of the charges and currents.

Thus the modern interpretation uses the picture that the sources are the charge-current distributions alone, as made explicit by the Jefimenko formlulas.

 

[DoobleD]

In an electrodynamic situation (a time-varying one such as an oscillating dipole), the electric field is associated with both electric charges and with time-varying magnetic fields (via Faraday's Law). The fields associated with time-varying magnetic fields tend to form loops, and do not "originate" on charges. The two kinds of electric fields superpose (add together) to produce a single field whose field lines have "mixed" characteristics: sometimes they originate on charges, and then they "break off".

Ahhh, that makes sense! Very clear answer again, appreciate your help!

(Have you studied electric flux and its mathematical definition yet?)

I have yes. Though sometimes a while after I learned and understood something, I kind of forget how it works when I suddenly face a new situation/concept (like EM waves here).

The analogy with the position graph is intuitive!

I'll keep in mind that fields drawings are just visualization tools mostly not accurate.

I appreciate all the help guys, Physics Forum is really efficient! Many questions answered.

 

[Dale]

I don't like this picture of saying the "electric field is associated with time-varying magnetic fields". It's quite misleading an interpretation of Faraday's Law,
$$\vec{\nabla} \times \vec{E}+\frac{1}{c} \partial_t \vec{B}=0.$$

There is nothing misleading about it at all. Look at the equation. The curl of the E field is indeed associated with at time-varying B field. That is simply what the equation says. I understand your preferences from other threads, but you are substantially overstating your case here.

you can rewrite these solutions such that, e.g., the time-varying magnetic field is treated as a source of the electric field

Note that this is not what is implied by the phrase "associated with". There is nothing in "associated with" that implies "is the source of" or "is the cause of".

 

[jtbell]

There is nothing in "associated with" that implies "is the source of" or "is the cause of".

In fact I chose the phrasing "associated with" for precisely that reason! Although the OP has probably seen "caused by" in his textbook(s), I wanted to avoid saying that because I knew it would be likely to trigger responses that would lead this thread off on a tangent.

 

[Dale]

I realize those illustrations can't be quantitatively precise, but I expect them to be accurate at least qualitatively. Otherwise they would be useless, I think. While they have not as much value as the equations, it is important to me to understand them, because they usually help me to get a feeling with the equations. And after all, they are just another tool to understand the physics.

I think that the problem is less whether they are quantitatively correct vs qualitatively correct and more about the fact that each illustration means something different. Do you recognize that the arrows and lines in the figure in post 1 have very different meanings than the arrows and lines in post 5? You have to read the corresponding text carefully to understand what is being represented in each case.

Field lines begin and end on charges, and yet the lines on post 5 begin and end in free space, so they are not the traditional field lines. Does the associated text with each figure give you some clues about this difference in the drawings?

 

[DoobleD]

Field lines begin and end on charges, and yet the lines on post 5 begin and end in free space, so they are not the traditional field lines. Does the associated text with each figure give you some clues about this difference in the drawings?

Not really sadly. It would have been great to read somewhere something like "careful those are not traditional field lines" about the pictures like in post 5. Even if it looks obvious.

Having those different representations definitely confused me. As you wrote, this was a source of problem. It is true that each picture should be carefully understood in its own context. Thanks for the advice.

 

[Dale]

So the E-field is a vector field, and vector fields are fundamentally difficult to draw on paper. As a result there are a variety of techniques used to visualize them. To understand the difficulty, I would encourage you to get some math software and try using even pre-packaged plotting functions to show them for some basic vector fields.

The E-field lines drawn on the figure in post 1 are so-called "streamlines". They are lines which have the property that the tangent to the curve at each point is in the same direction as the vector field at that point. Streamlines, by themselves, do not provide any information about the magnitude of the vector field, only its direction.

The E-field lines drawn on the figure in post 5 are vector field plot lines. The direction and length of the arrows directly represent the direction and the magnitude of the vector field, evaluated at the point where the tail is located. There is no information provided about any points anywhere other than exactly on the z axis.

 

[vanhees71]

Though shalt not make images ;-)). Just calculate the the electric dipole field, using the retarded potential. For a plane-wave mode of frequency $\omega$ it leads to an electric field,
$$\vec{E}(t,\vec{r})=\vec{E}'(\vec{r}) \exp(-\mathrm{i} \omega t)$$
with
$$\vec{E}'(\vec{r})=\frac{q}{4 \pi r^3} \left [\frac{3-\mathrm{i} k r-k^2 r^2}{r^2} \vec{r} (\vec{r} \cdot \vec{d})-(1-\mathrm{i} k r - k^2 r^2)\vec{d} \right ] \exp(\mathrm{i} k r),$$
$$\vec{B}'(\vec{r})=-\frac{\mathrm{i}k q}{r^3}(\mathrm{i} kr -1) \exp(\mathrm{i} k r).$$
Here the dipole moment is written as $q \vec{d} \exp(-\mathrm{i} \omega t)$ and $k=\omega/c$. The solution clearly shows that the sources are the oscillating charge-current distributions,
$$\rho(t,\vec{r}=-q \vec{d} \cdot \vec{\nabla} \delta(\vec{r}) \exp(-\mathrm{i} \omega t), \quad \vec{j}=-\mathrm{i} q \omega \vec{d} \delta^{(3)}(\vec{r}).$$

For $k r=2 \pi r/\lambda \ll 1$ we find a static electric dipole field which is oscillating synchronous and a magnetic field which oscillates with a relative phase shift of $\pi/2$ with the dipole:
$$\vec{E}'(\vec{r}) \simeq \frac{q}{4 \pi r^3} [3\hat{r} (\hat{r} \cdot \vec{d})-\vec{d}],$$
$$\vec{B}'(\vec{r}) \simeq \frac{\mathrm{i} k}{4 \pi r^2} q \hat{r} \times \vec{d}.$$
The near field goes like $1/r^3$ like a static electric dipole field.

For $k r \gg 1$ we find
$$\vec{E}'(\vec{r})=\frac{k^2}{2 \pi r} [\vec{d}-\hat{x}(\hat{r} \cdot \vec{d})] \exp(\mathrm{i} k r),$$
$$\vec{B'}(\vec{r})=\hat{r} \times \vec{E}'.$$
The far field is thus like a spherical wave going like $1/r$ with an amplitude modulated by the typical dipole characteristics.

Just one remark on Einstein causality:

That the near fields are synchronous with the dipole oscillations without retardation, however, must not be mistaken as indicating instantaneous action as a distance, but it's the near-field approximation of a stationary state, i.e., the here given solution is one, where the oscillation of the dipole was switched on asymptotically in the very far past, $t_0 \rightarrow -\infty$. To get a solution for the case that the dipole oscillation was started at $t=0$ you have to use a Fourier transformation for the source,
$$\vec{j}(t,\vec{r})=-\mathrm{i} q \vec{d} \int_{\mathbb{R}} \frac{\mathrm{d} \omega}{2 \pi} A(\omega) \omega \exp(-\mathrm{i} \omega t),$$
where $A(\omega)$ is sufficiently quickly falling for $\omega \rightarrow \pm \infty$ and as an analytic function must have poles only in the lower complex $\omega$ plane. Due to the exponential in the Fourier integral one has to close the contour in the upper plane for $t<0$ and then you have $\vec{j}(t,\vec{r})=0$ for $t<0$. Now the very same Fourier integration has to be done for the electromagnetic field, and doing this integral for the exact solution, including the spatial exponential $\exp(\mathrm{i} k r)=\exp(\mathrm{i} \omega c r)$ shows that the wave front propagates exactly with the speed of light everywhere, i.e., for $kr-\omega t>0$ the electromagnetic field is 0, i.e., there is no field earlier than "allowed" by the relativistic "speed limit".

 

[DoobleD]

So the E-field is a vector field, and vector fields are fundamentally difficult to draw on paper. As a result there are a variety of techniques used to visualize them. To understand the difficulty, I would encourage you to get some math software and try using even pre-packaged plotting functions to show them for some basic vector fields.

The E-field lines drawn on the figure in post 1 are so-called "streamlines". They are lines which have the property that the tangent to the curve at each point is in the same direction as the vector field at that point. Streamlines, by themselves, do not provide any information about the magnitude of the vector field, only its direction.

The E-field lines drawn on the figure in post 5 are vector field plot lines. The direction and length of the arrows directly represent the direction and the magnitude of the vector field, evaluated at the point where the tail is located. There is no information provided about any points anywhere other than exactly on the z axis.

Thank you for the explanations.

I've played a little with some MIT field lines software and visualization tools available online, they are nice to get a feeling on those things. In case someone passing by is interested, there's a lot of different links for those, like here, here, or here, or in some sections here. This is not exhaustive.