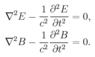From Maxwell's equations to EM waves

[iVenky]

Hi,

I just finished studying Maxwell's equations. Based on my understanding, when you solve maxwell's equation, you get the wave equation and it simplies to

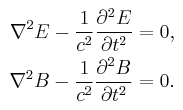
in a charge and current-free region.

I understand that these two equations are similar to an equation of a wave in space. What I am failing to understand is in connecting the dots between EM radiation (like in radios) and this specific equation. Like, I got the following questions,

1) Electric fields (and Magnetic Fields), that constitute current in a wire, always propagate as a wave (whether it's inside a conductor or outside), right? Is there any specific condition for EM radiation (E & B fields escape from a conductor into free space) to happen? Like for example, I see EM waves get detached from the wire and starting to propagate in free space below (source wiki). What's so special about an antenna? I have seen examples where we have open-ended circuits to get EM radiation (is it necessary?).

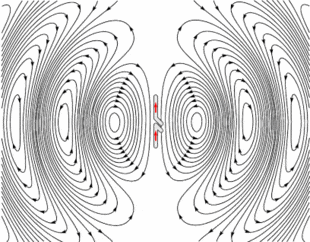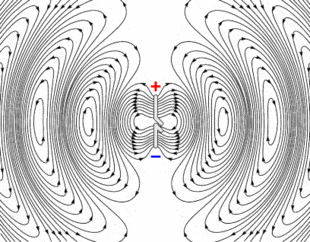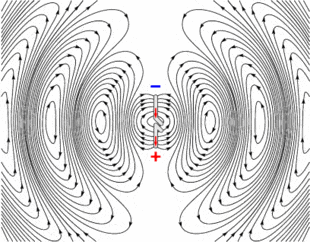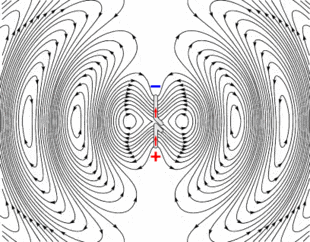
2) I don't see any frequency dependency in the above wave equation and it suggests you always have an EM radiation irrespective of the frequency of the signal. However, what I know is as we go to higher frequencies, the EM radiation is more pronounced (unlike DC for example).
3) E and B fields are always perpendicular? And are they always in phase in time at a given point? If I somehow suppress the E field in space, would it also suppress the B fields? Are they interdependent?

If someone can answer me the questions, that would greatly help me.

 

[Orodruin]

The wave equation you have written down ignores the source and just describes the propagation of EM waves. Without the source terms, you will only be able to describe freely propagating waves. Not how those waves interact with matter.

I understand that these two equations are similar to an equation of a wave in space.

They are not similar to an equation of a wave in space. They are the wave equation.

We always have EM radiation, whether it's just a wire or an antenna (the equation doesn't distinguish these), right?

Your equation does not describe the interaction with matter so your equation describes neither. If you would have included the source term, you would have seen that the source depends on the motion of electromagnetic charges. The point with an antenna is to make EM charges move in such a way that they produce a fair amount of electromagnetic radiation.

2) I don't see any frequency dependency in the above wave equation and it suggests you always have an EM radiation irrespective of the frequency of the signal. However, what I know is as we go to higher frequencies, the EM radiation is more pronounced (unlike DC for example).

There is no frequency dependence in the wave equation. Any difference in behaviour comes from the interaction with matter.

3) E and B fields are always perpendicular? And are they always in phase in time at a given point? If I somehow suppress the E field in space, would it also suppress the B fields?

For a radiation field, yes. Your equations do not show this, but Maxwell's equations do.

 

[jtbell]

I don't see any frequency dependency in the above wave equation and it suggests you always have an EM radiation irrespective of the frequency of the signal.

An electromagnetic wave (indeed any kind of wave) does not even need to be periodic. Consider the function $E = E_0 f(x-ct)$ where $f$ is an arbitrary function. $f$ might represent a sinusoidal curve, or a more generally periodic curve such as a sawtooth, or just a random squiggle. Substitute it into the wave equation for $E$ and you'll find that it's a solution. It's the most general "plane wave" that propagates in the +x direction.

 

[iVenky]

The wave equation you have written down ignores the source and just describes the propagation of EM waves. Without the source terms, you will only be able to describe freely propagating waves. Not how those waves interact with matter.

Your equation does not describe the interaction with matter so your equation describes neither. If you would have included the source term, you would have seen that the source depends on the motion of electromagnetic charges. The point with an antenna is to make EM charges move in such a way that they produce a fair amount of electromagnetic radiation.

Thank you very much for the reply. So I assumed a charge-free region and that's why my equations don't explain the behavior of interaction with matter. Can you tell me what happens once I include the charge density term and how it explains the behavior of an antenna or a wire? Is there any specific condition for EM radiation to happen?

 

[trurle]

Thank you very much for the reply. So I assumed a charge-free region and that's why my equations don't explain the behavior of interaction with matter. Can you tell me what happens once I include the charge density term and how it explains the behavior of an antenna or a wire? Is there any specific condition for EM radiation to happen?

You need to add "displacement current" part to Maxwell equations to get from antenna current to EM radiation. Vacuum act as polarizable dielectric, and therefore do support displacement current.
As about specific criteria for radiation, you should search for "Chu-Harrington limit".

 

[iVenky]

You need to add "displacement current" part to Maxwell equations to get from antenna current to EM radiation. Vacuum act as polarizable dielectric, and therefore do support displacement current.
As about specific criteria for radiation, you should search for "Chu-Harrington limit".

Thanks, so in this expression

[tex] \nabla^2 E - \mu_0 \epsilon_0 \frac{ \partial^2 E}{\partial t^2} = \nabla \frac{\rho}{\epsilon_0} + \mu_0 \bf{ \frac{\partial J}{\partial t} } [/tex]

the bold item indicates the displacement current that's causing the radiation, right?
My question is, in this figure

We have a dipole antenna, you can see that the E field cuts off from its source becoming EM radiation. This is the part that I want to know. Is there a frequency or a condition for the signal parameters to cut off from its source or it cuts always? Does the strength/power of the EM wave depend on the frequency?

 

[tech99]

You need to add "displacement current" part to Maxwell equations to get from antenna current to EM radiation. Vacuum act as polarizable dielectric, and therefore do support displacement current.
As about specific criteria for radiation, you should search for "Chu-Harrington limit".

In the case of a loop of wire which is radiating, where is the displacement current? So far as I know, the radiation originates from accelerating charges in the wire. It seems not specifically necessary to have a capacitor (and hence displacement currents) in an antenna.
The electric field associated with a series capacitor (as between the arms of a dipole) seems to be in quadrature to the radiated electric field, so is presumably not part of the radiation mechanism.
Further, if displacement current radiated, the current flowing in the capacitance between the arms of a dipole would cancel the radiation from the conductors - but it doesn't.

 

[Delta2]

Thanks, so in this expression

[tex] \nabla^2 E - \mu_0 \epsilon_0 \frac{ \partial^2 E}{\partial t^2} = \nabla \frac{\rho}{\epsilon_0} + \mu_0 \bf{ \frac{\partial J}{\partial t} } [/tex]

the bold item indicates the displacement current that's causing the radiation, right?

The bold term is the current density $\vec{J}$ which needs to be time varying so that its time derivative $\frac{\partial \vec{J}}{\partial t}$ is not zero so that it acts as a source for an EM-wave. The equation you just wrote is the non-homogeneous wave equation and the right hand side of the equation is called the source term of the wave equation. So any time varying current density $J$ with non vanishing first time derivative will act as a source of an EM-wave, but the point of constructing an antenna is to give such a shape to the function of current density $\vec{J}(\vec{r},t)$ in order to maximize the power radiated into the EM-wave. For example if we have a current density of the form $\vec{J}(\vec{r},t)=\vec{J_0}\sin(\omega t-\vec{k}\cdot\vec{r})$ its first time derivative will be $\omega\vec{J_0}\cos(\omega t-\vec{k}\cdot\vec{r})$ so you can get a first idea how the strength of an EM wave depends on the frequency of the current density.

The displacement current is the term $\frac{\partial E}{\partial t}$ that appears in the Maxwell-Ampere equation (the 4th equation from Maxwell's equation), and without this term , it is not possible to arrive to the non homogeneous wave equation (starting from the Maxwell's equations and with mathematical processing using vector calculus), which you write at the start of this post.

 

[iVenky]

The bold term is the current density $\vec{J}$ which needs to be time varying so that its time derivative $\frac{\partial \vec{J}}{\partial t}$ is not zero so that it acts as a source for an EM-wave. The equation you just wrote is the non-homogeneous wave equation and the right hand side of the equation is called the source term of the wave equation. So any time varying current density $J$ with non vanishing first time derivative will act as a source of an EM-wave, but the point of constructing an antenna is to give such a shape to the function of current density $\vec{J}(\vec{r},t)$ in order to maximize the power radiated into the EM-wave. For example if we have a current density of the form $\vec{J}(\vec{r},t)=\vec{J_0}\sin(\omega t-\vec{k}\cdot\vec{r})$ its first time derivative will be $\omega\vec{J_0}\cos(\omega t-\vec{k}\cdot\vec{r})$ so you can get a first idea how the strength of an EM wave depends on the frequency of the current density.

The displacement current is the term $\frac{\partial E}{\partial t}$ that appears in the Maxwell-Ampere equation (the 4th equation from Maxwell's equation), and without this term , it is not possible to arrive to the non homogeneous wave equation (starting from the Maxwell's equations and with mathematical processing using vector calculus), which you write at the start of this post.

Thanks. That's a good explanation. So, fundamentally, as we go to higher frequencies the displacement current increases, which increases the power radiated as EM waves, right? Is there any specific condition for detachment of EM waves from the wire (like the figure shown above)? or that it happens for any frequency and it's just that the strength of EM wave is increasing as the frequency increases.

 

[Delta2]

Thanks. That's a good explanation. So, fundamentally, as we go to higher frequencies the displacement current increases, which increases the power radiated as EM waves, right? Is there any specific condition for detachment of EM waves from the wire (like the figure shown above)? or that it happens for any frequency and it's just that the strength of EM wave is increasing as the frequency increases.

As we go to higher frequencies the term $\frac{\partial{\vec{J}}}{\partial t}$ increases which increases the power radiated as EM waves. The displacement current term $\frac{\partial\vec{E}}{\partial t}$ will also increase but the displacement current is not considered the source of the EM wave (its not in the source term of the wave equation). The displacement current term is part of the internal mechanism of time varying electric and magnetic fields that makes them transmit like a wave, as I said before it is needed in order to prove from Maxwell's equations that the electric and magnetic field satisfy the wave equation.
There isn't any specific condition for detachment of em waves from a wire that carries a current density , other than that the current density is time varying. But the strength of the em wave depends not only on frequency but on the shape of the wire as well. In general it depends on the exact form of the function of current density $\vec{J}(\vec{r},t)$. For example if we have a wire of fixed length and we make a solenoid coil with many turns out of it, then this solenoid coil will not radiate much. On the other hand if we make just one big turn (with the same total length of wire) this single loop will radiate much better (it acts as a magnetic dipole antenna).