- #1
mohabitar
- 140
- 0
How were they able to derive this?
The sequence in this sum is a geometric sequence.mohabitar said: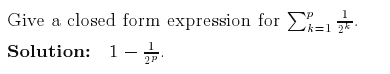
How were they able to derive this?
mohabitar said:None, I really don't see what you did from the 2nd step to the third step.
mohabitar said:Why would we subtract 1/2sp from sp? Can we just make a quick generalization? There was a trick to it that I forgot. If the summation starts at 1 and you want it to start at 0, then just take out the first term, or something like that? But now I still don't get the original question. Any other way to explain-you guys are really complicating this thing.
A closed form summation is a mathematical expression that represents the sum of a finite series of numbers. It is also known as an exact solution, as it provides an explicit formula for calculating the sum rather than relying on iterative or recursive methods.
Understanding the derivation of closed form summation allows us to efficiently and accurately calculate the sum of a series without having to manually add up each individual term. It also provides insight into the underlying mathematical principles and can be applied to various fields such as physics, engineering, and finance.
The derivation of closed form summation involves using mathematical techniques such as algebra, calculus, and geometric series to manipulate the series expression into a simpler and more manageable form. This process may also involve identifying patterns and using known formulas to simplify the expression.
No, closed form summation can only be applied to series that have a finite number of terms and follow a specific pattern or sequence. Some examples of series that can be solved using closed form summation include arithmetic series, geometric series, and power series.
Yes, there are alternative methods such as using recursive formulas or numerical approximations such as the trapezoidal rule or Simpson's rule. However, closed form summation is considered the most efficient and accurate method for calculating the sum of a series, especially for larger series with a large number of terms.