Discussing the Near Step Function for γ=0.4823241136337762

[AntonVrba]

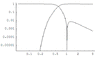
I would like to invite comment to the near step function below.

<br /> \Mvariable{step(x)}=\frac{{e^{-\frac{\gamma }{{x^2}}}}}{{\sqrt{1-\frac{{e^{-\frac{\gamma }{{x^2}}}}}{{x^2}}}}}<br />

the above function evaluates to nearly 1 for |x|>1 and nearly zero for |x|<0.3

for gamma = 0.4823241136337762 I have attached the plots of step and 1-step

here are some spot values for
x and step(x)
0.05 1.15E-83
0.1 1.84E-21
0.2 6.55E-6
0.3 5.11E-3
0.4 6.11E-2
0.5 2.32E-1
0.6 0.518
0.8 0.932
1.0 1.0068
2.0 1.006
5.0 1.00092
10 1.00022
50 1.0000090

 

[Data]

Indeed. If you change all the x^2s to x^4s (or x^{1000}s), then it'll get even closer to a step function.

 

[AntonVrba]

I just noticed that the step function can be simplified even more
<br /> \Mvariable{step}(x)=<br /> \frac{{e^{-\frac{\gamma }{{x^2}}}}}{{\sqrt{1-\frac{{e^{-\frac{\gamma }{{x^2}}}}}{{x^2}}}}}<br /> <br /> =\frac{{{\alpha}^{\frac{1}{{x^2}}}}}{{\sqrt{1-\frac{{{\alpha}^{\frac{1}{{x^2}}}}}{{x^2}}}}}\\<br />

for above gamma= 0.4823241136337762 , alpha =0.61734693877551, hence

<br /> \Mvariable{step}(x)=<br /> \frac{{{0.61734693877551}^{\frac{1}{{x^2}}}}}{{\sqrt{1-\frac{{{0.61734693877551}^{\frac{1}{{x^2}}}}}{{x^2}}}}}\\<br />

 

[Data]

Well, it's not really "simpler." You have the same number of arbitrary constants, though I guess you have a couple fewer symbols in general (you got rid of two minus signs - but you could do that just by specifying that \gamma must be negative). I'd usually just leave it in the exponential form, but that's a subjective choice based on the fact that I like the letter e

 

[AntonVrba]

Well, it's not really "simpler." You have the same number of arbitrary constants, QUOTE]


arbitrary
just play with the function and you will see that gamma or alpha has a rather very limited range for the function not to become complex for any real number

By proper choice of the Alpha you can make the function overshoot (become slightly larger than one) as in the example given, or the function always remaining slightly less than one i.e approach one at infinity, and that in a only very limitted range of values.

 

[Data]

arbitrary within a certain domain is what I should have said, of course. In this case, you need \gamma &gt; 1/e.