natedigity
- 6
- 0
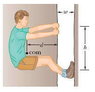
In Figure 12-42 a 57 kg rock climber is in a lie-back climb along a fissure, with hands pulling on one side of the fissure and feet pressed against the opposite side. The fissure has width w = 0.15 m, and the center of mass of the climber is a horizontal distance d = 0.50 m from the fissure. The coefficient of static friction between hands and rock is μ1 = 0.45, and between boots and rock it is μ2 = 1.25. The climber adjusts the vertical distance h between hands and feet until the (identical) pull by the hands and push by the feet is the least that keeps him from slipping down the fissure. (He is on the verge of sliding.)
What is the value of h?
mg of the climber is 558.6N
What is the magnitude of the climber’s pull by his hands and push by his shoes? This is the same question as one asking for the magnitude of the normal force at his hands and shoes when he is on the verge of sliding.
Number 328.588 Units N
I have found the tourques using the foot/rock contact as my pivot point.
What are the torques due to (a) the frictional force on the hands, (b) the frictional force on the shoes, (c) the normal force on the shoes, and (d) the gravitational force on the climber, taken to act at the com? Include a minus sign if a torque is negative.
(a) Number -22.1797 Units N•m
(b) Number 0 Units N•m
(c) Number 0 Units N•m
(d) Number 363.09 Units N•m
The torque due to the climber’s pull by the hands on the fissure wall? That is, what is the torque due to the normal force on his hands? This is -340.91 Nm
I am confused on how to find the distance h as in the height in the y direction with the above torques. I am sure I am missing something stupid. Thanks, Nathan.
What is the value of h?
mg of the climber is 558.6N
What is the magnitude of the climber’s pull by his hands and push by his shoes? This is the same question as one asking for the magnitude of the normal force at his hands and shoes when he is on the verge of sliding.
Number 328.588 Units N
I have found the tourques using the foot/rock contact as my pivot point.
What are the torques due to (a) the frictional force on the hands, (b) the frictional force on the shoes, (c) the normal force on the shoes, and (d) the gravitational force on the climber, taken to act at the com? Include a minus sign if a torque is negative.
(a) Number -22.1797 Units N•m
(b) Number 0 Units N•m
(c) Number 0 Units N•m
(d) Number 363.09 Units N•m
The torque due to the climber’s pull by the hands on the fissure wall? That is, what is the torque due to the normal force on his hands? This is -340.91 Nm
I am confused on how to find the distance h as in the height in the y direction with the above torques. I am sure I am missing something stupid. Thanks, Nathan.