Lexielai
- 3
- 0
Warning! Posting template must be used for homework questions.
Hey everyone!
I'm new to this site, but I figured I might as well start it off with a bang and go straight into the nitty-gritty. This is a problem from the homework assignment I've been given for tonight, and although I can sort of see that it can be solved, the right series of equations to use is seriously eluding me.
From the top of a tall building, a gun is fired. The bullet leaves the gun at a speed of 340 m/s, parallel to the ground. As the drawing shows, the bullet puts a hole in a window of another building and hits the wall that faces the window. Using the data in the drawing, determine the distances D and H, which locate the point where the gun was fired. Assume that the bullet does not slow down as it passes through the window.
Drawing:
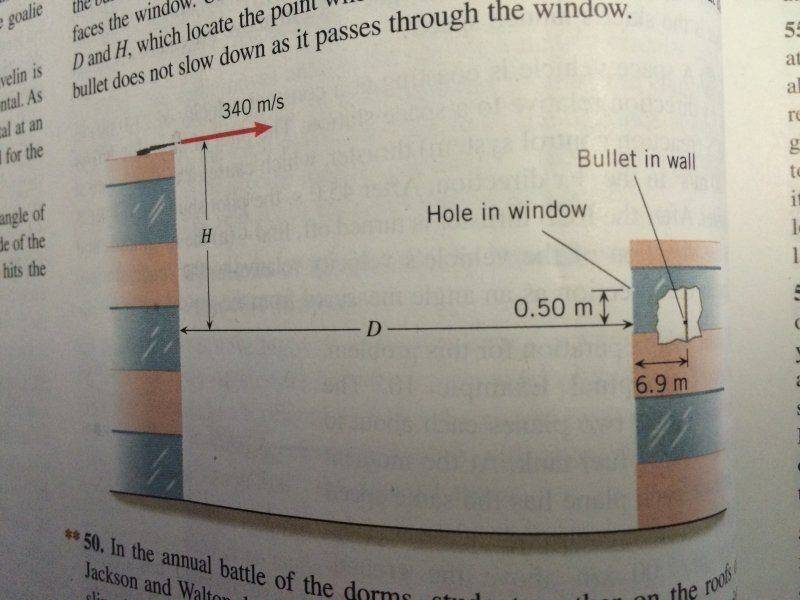
I wasn't too sure about how to proceed with this one. At first I took a look at the drawing and assumed that the place the bullet landed in was at exactly at the bottom of the 0.50 m window such that if a line was drawn between the window and the wall, the bullet would lie exactly on that line. (Not sure if this was unreasonable for me to assume, but I didn't know if there was another way to figure out the bullet's landing location)
In order for the assumption I made above to be true, then the projectile's velocity had to be such that it would travel 6.9 m horizontally in the time it took to travel -0.5 m vertically. Unfortunately I then realized I didn't know the initial velocity for that, because the projectile was already in flight for an unspecified period of time; as the problem explicitly states that the projectile would not be slowed by impact, the velocity when it impacted the window would not be 0. Thus I could not calculate the velocity from impact against the window to striking the wall.
I also thought about splitting the figure shown into two shapes: one triangle and one rectangle. The triangle would have a height of H-0.5m and the length would be D, while the rectangle would have a length of D and a height of 0.5m. Then I would use the position equation (Y = Yinitial + Vinitialt + 1/2(g)(t)2) to calculate the time it took to reach the 0.5m window. However, I then realized that I didn't know the distance between the top of the building to that window, so I was once again stumped.
Maybe there's something obvious here that I'm overlooking, but I'd appreciate a second look by one of you fine gentlemen or ladies.
Thanks in advance!
I'm new to this site, but I figured I might as well start it off with a bang and go straight into the nitty-gritty. This is a problem from the homework assignment I've been given for tonight, and although I can sort of see that it can be solved, the right series of equations to use is seriously eluding me.
From the top of a tall building, a gun is fired. The bullet leaves the gun at a speed of 340 m/s, parallel to the ground. As the drawing shows, the bullet puts a hole in a window of another building and hits the wall that faces the window. Using the data in the drawing, determine the distances D and H, which locate the point where the gun was fired. Assume that the bullet does not slow down as it passes through the window.
Drawing:
I wasn't too sure about how to proceed with this one. At first I took a look at the drawing and assumed that the place the bullet landed in was at exactly at the bottom of the 0.50 m window such that if a line was drawn between the window and the wall, the bullet would lie exactly on that line. (Not sure if this was unreasonable for me to assume, but I didn't know if there was another way to figure out the bullet's landing location)
In order for the assumption I made above to be true, then the projectile's velocity had to be such that it would travel 6.9 m horizontally in the time it took to travel -0.5 m vertically. Unfortunately I then realized I didn't know the initial velocity for that, because the projectile was already in flight for an unspecified period of time; as the problem explicitly states that the projectile would not be slowed by impact, the velocity when it impacted the window would not be 0. Thus I could not calculate the velocity from impact against the window to striking the wall.
I also thought about splitting the figure shown into two shapes: one triangle and one rectangle. The triangle would have a height of H-0.5m and the length would be D, while the rectangle would have a length of D and a height of 0.5m. Then I would use the position equation (Y = Yinitial + Vinitialt + 1/2(g)(t)2) to calculate the time it took to reach the 0.5m window. However, I then realized that I didn't know the distance between the top of the building to that window, so I was once again stumped.
Maybe there's something obvious here that I'm overlooking, but I'd appreciate a second look by one of you fine gentlemen or ladies.
Thanks in advance!