davidgruty
- 20
- 0
Hello all!
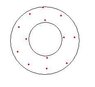
I am designing a plate to hold some crystals, bla, bla...
The point is that this mounting plate is held by other plate by let's say "interface" pieces.
I made some calculations and I need 24 pieces (6 by quadrant) to be on the safe side.
I do not know how share them over the surface homogeneously.
Does anyone have any idea??
thank you
Cheers,
I am designing a plate to hold some crystals, bla, bla...
The point is that this mounting plate is held by other plate by let's say "interface" pieces.
I made some calculations and I need 24 pieces (6 by quadrant) to be on the safe side.
I do not know how share them over the surface homogeneously.
Does anyone have any idea??
thank you
Cheers,