jweica
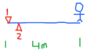
- 5
- 1
The board is 4m and has 2 supports: support 1 exerts 5400N and support 2 exerts 6000N before the diver performs the dive.
Neglecting the mass of the board, what is the force on the board due to the weight of the diver?
My attempt at this question: FS2 - FS1 = 6000 - 5400 = 600N
But I'm having difficulty on solving this question due to not really understanding on what to do with the given information...
Thanks!
Neglecting the mass of the board, what is the force on the board due to the weight of the diver?
My attempt at this question: FS2 - FS1 = 6000 - 5400 = 600N
But I'm having difficulty on solving this question due to not really understanding on what to do with the given information...
Thanks!