FallenApple
- 564
- 61
I ask this because of this diagram.
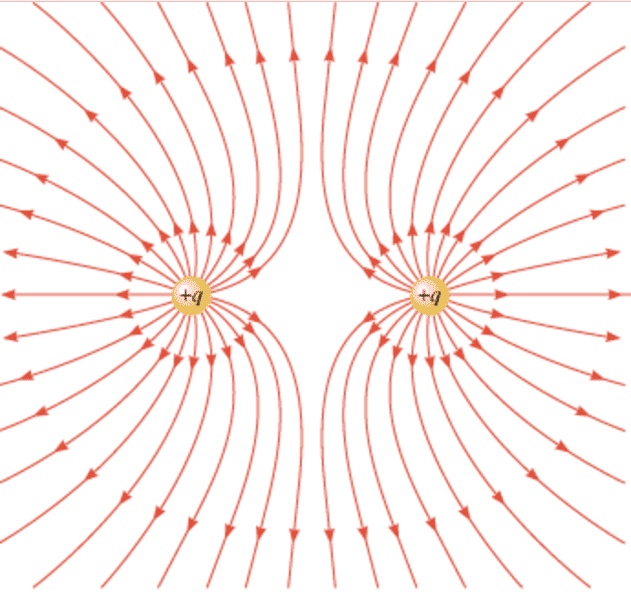
Say that two charges are held a certain distance apart and are let go. Well, we see that the field lines of one charge repels the other.
And I noticed that the field lines for an accelerating charge also bends.
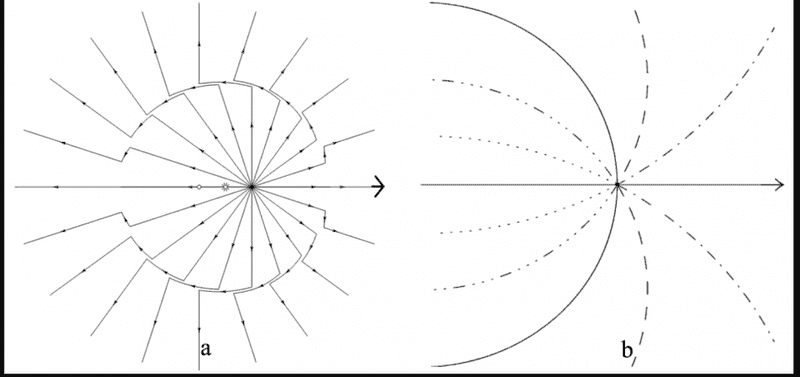
So can we say that because one field changes the geometric configuration of the other field, the other charge must accelerate to accompany that change?
I know the formal definition involves charges(F=qE), but I want to know if it can be viewed from another perspective.
Say that two charges are held a certain distance apart and are let go. Well, we see that the field lines of one charge repels the other.
And I noticed that the field lines for an accelerating charge also bends.
So can we say that because one field changes the geometric configuration of the other field, the other charge must accelerate to accompany that change?
I know the formal definition involves charges(F=qE), but I want to know if it can be viewed from another perspective.