- #1
zonde
Gold Member
- 2,961
- 224
This question came up in another thread.
I don't see where the probability shows up in Nick Herbert's proof.
For discussion of Eberhard's proof I will give it in this post:
Eberhard inequality for detection efficiency ##\eta## < 100%
Bell inequalities concern expectation values of quantities that can be measured in four different experimental setups, defined by specific values ##\alpha_1##, ##\alpha_2##, ##\beta_1##, and ##\beta_2## of ##\alpha## and ##\beta##. The setups will be referred to by the symbols ##(\alpha_1, \beta_1)##, ##(\alpha_1, \beta_2)##, ##(\alpha_2, \beta_1)##, and ##(\alpha_2, \beta_2)##, where the first index designates the value of ##\alpha##. and the second index the value of ##\beta##.
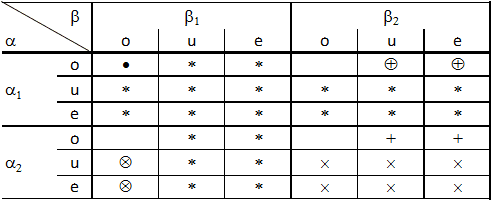
In each setup, the fate of the photon a and the fate of photon b is referred to by an index (o) for photon detected in the ordinary beam, (e) for photon detected in the extraordinary beam, or (u) for photon undetected. Therefore there are nine types of events: (o, o), (o, u), (o, e), (u, o), (u, u), (u, e), (e, o), (e, u), and (e, e), where the first index designates the fate of photon a and the second index the fate of photon b. Table I shows a display of boxes corresponding to the nine types of event in each setup. The value of ##\alpha##, and the fate of photon a designate a row. The value of ##\beta## and the fate of photon b designate a column. Any event obtained in one of the setups corresponds to one box in Table I.
For a given theory, we consider all the possible sequences of N events that can occur in each setup. N is the same for the four setups and arbitrarily large. As in [Eberhard1977] and [Eberhard1978], a theory is defined as being "local" if it predicts that, among these possible sequences of events, one can find four sequences (one for each setup) satisfying the following conditions:
(i) The fate of photon a is independent of the value of ##\beta##, i.e., is the same in an event of the sequence corresponding to setup ##(\alpha_1, \beta_1)## as in the event with the same event number k for ##(\alpha_1, \beta_2)##; also same fate for a in ##(\alpha_2, \beta_1)## and ##(\alpha_2, \beta_2)##; this is true for all k's for these carefully selected sequences.
(ii) The fate of photon b is independent of the value of ##\alpha##, i.e., is the same in event k of sequences ##(\alpha_1, \beta_1)## and ##(\alpha_2, \beta_1)##; also same fate for b in sequences ##(\alpha_1, \beta_2)## and ##(\alpha_2, \beta_2)##.
(iii) Among all sets of four sequences that one has been able to find with conditions (i) and (ii) satisfied, there are some for which all averages and correlations differ from the expectation values predicted by the theory by less than, let us say, ten standard deviations.
These conditions are fulfilled by a deterministic local hidden-variable theory, i.e., one where the fate of photon a does not depend on ##\beta## and the fate of b does not depend on ##\alpha##. For such a theory, these four sequences could be just four of the most common sequences of events generated by the same values of the hidden variables in the different setups. Conditions (i)—(iii) are also fulfilled by probabilistic local theories, which assign probabilities to various outcomes in each of the four setups and assume no "influence" of the angle ##\beta## on what happens to a and no "influence" of ##\alpha## on b. With such theories, one can generate sequences of events having properties (i) and (ii) by Monte Carlo, using an algorithm that decides the fate of a without using the value of ##\beta## and, for b, without using the value of ##\alpha##. If the same random numbers are used for the four different setups, the sequences of events will automatically have properties (i) and (ii), and the vast majority of them will have property (iii).
Let us follow an argument first used in Ref. [Stapp1971]. When four sequences are found satisfying conditions (i) and (ii), the four events with the same event number k in the four different sequences will be called "conjugate events". Because of condition (i), two conjugate events in setups ##(\alpha_1, \beta_1)## and ##(\alpha_1, \beta_2)## fall into two boxes on the same row in Table I. The same thing applies for conjugate events in setups ##(\alpha_2, \beta_1)## and ##(\alpha_2, \beta_2)##. Because of (ii), conjugate events for setups ##(\alpha_1, \beta_1)## and ##(\alpha_2, \beta_1)## lie in boxes in the same column; and so do conjugate events for ##(\alpha_1, \beta_2)## and ##(\alpha_2, \beta_2)##. Let us select all the ##n_{oo}(\alpha_1, \beta_1)## events that fall into the box marked with a ##\bullet## in the section of Table I reserved for setup ##(\alpha_1, \beta_1)##. None of these events falls into any other box for setup ##(\alpha_1, \beta_1)##. Because of condition (i), their conjugate events in setup ##(\alpha_1, \beta_2)## fall into boxes on row o. Because of condition (ii), the conjugate events in setup ##(\alpha_2, \beta_1)## lie in boxes in column o. Therefore none of the boxes marked with a ##*## contains any of the events of this sample or any of their conjugates.
Now, from that sample, let us remove events with conjugates falling in one of the boxes marked with a ##\otimes## in setup ##(\alpha_2, \beta_1)##. The number of events subtracted is smaller than or equal to the total number ##n_{uo}(\alpha_2, \beta_1)## + ##n_{eo}(\alpha_1, \beta_1)## of events of all categories contained in those two boxes. Therefore the remaining sample contains ##n_{oo}(\alpha_1, \beta_1) — n_{uo}(\alpha_2, \beta_1) — n_{eo}(\alpha_2, \beta_1)## events or more. None of the events in the remaining sample has a conjugate falling in a box on rows u or e in setup ##(\alpha_2, \beta_1)##; thus, because of condition (i), none falls in setup ##(\alpha_2, \beta_2)## either. None of the conjugate events falls in a box marked with an ##\times## .
Let us further restrict the sample by removing events with conjugates in sequence ##(\alpha_1, \beta_2)## falling in boxes marked with a ##\oplus## in Table I. Using the same argument as in the preceding paragraph, the number of events left must be more than or equal to
##n_{oo}(\alpha_1, \beta_1) — n_{uo}(\alpha_2, \beta_1) — n_{eo}(\alpha_2, \beta_1) — n_{ou}(\alpha_1, \beta_2) — n_{oe}(\alpha_1, \beta_2)##
where ##n_{ou}(\alpha_1, \beta_2) + n_{oe}(\alpha_1, \beta_2)## is the total number of events of all categories falling into the boxes marked with a ##\oplus##. None of the events in that restricted sample falls in column u and e in setup ##(\alpha_1, \beta_2)##; therefore, because of condition (ii), none falls in setup ##(\alpha_2, \beta_2)## either; therefore, none falls in any box marked with a ##+## .
All events belonging to the latter sample must have conjugates in sequence ##(\alpha_2, \beta_2)## falling into the only remaining box for that setup, i.e., box (o,o). That is possible only if that most restricted sample contains a number of events less than or equal to the total number ##n_{oo}(\alpha_2, \beta_2)## of events of all categories in that box. Thus conditions (i) and (ii) can be satisfied by our four sequences only if
##n_{oo}(\alpha_1, \beta_1) — n_{uo}(\alpha_2, \beta_1) — n_{eo}(\alpha_2, \beta_1) — n_{ou}(\alpha_1, \beta_2) — n_{oe}(\alpha_1, \beta_2) \leq n_{oo}(\alpha_2, \beta_2)## (12)
i.e.,
##\mathit{J_B} = n_{oe}(\alpha_1, \beta_2) + n_{ou}(\alpha_1, \beta_2) + n_{eo}(\alpha_2, \beta_1) + n_{uo}(\alpha_2, \beta_1) + n_{oo}(\alpha_2, \beta_2) - n_{oo}(\alpha_1, \beta_1) ## (13)
For condition (iii) to be true no matter how large the number of events N is, inequality (13) also has to apply to the expectation values of these numbers. It is a form of the Bell inequality, which Eqs. (6)—(9) make equivalent to inequality (4) of Ref. [CH1974].
I will post again the link to Nick Herbert's proof here: https://www.physicsforums.com/threads/a-simple-proof-of-bells-theorem.417173/#post-2817138bhobba said:You miss the point - his [Nick Herbert's] proof, right or wrong, regardless of what you think of him, used probability.
If you want to discuss Eberhard' proof post the full proof and in another thread at least at the I level then it can be discussed.
I don't see where the probability shows up in Nick Herbert's proof.
For discussion of Eberhard's proof I will give it in this post:
Eberhard inequality for detection efficiency ##\eta## < 100%
Bell inequalities concern expectation values of quantities that can be measured in four different experimental setups, defined by specific values ##\alpha_1##, ##\alpha_2##, ##\beta_1##, and ##\beta_2## of ##\alpha## and ##\beta##. The setups will be referred to by the symbols ##(\alpha_1, \beta_1)##, ##(\alpha_1, \beta_2)##, ##(\alpha_2, \beta_1)##, and ##(\alpha_2, \beta_2)##, where the first index designates the value of ##\alpha##. and the second index the value of ##\beta##.
In each setup, the fate of the photon a and the fate of photon b is referred to by an index (o) for photon detected in the ordinary beam, (e) for photon detected in the extraordinary beam, or (u) for photon undetected. Therefore there are nine types of events: (o, o), (o, u), (o, e), (u, o), (u, u), (u, e), (e, o), (e, u), and (e, e), where the first index designates the fate of photon a and the second index the fate of photon b. Table I shows a display of boxes corresponding to the nine types of event in each setup. The value of ##\alpha##, and the fate of photon a designate a row. The value of ##\beta## and the fate of photon b designate a column. Any event obtained in one of the setups corresponds to one box in Table I.
For a given theory, we consider all the possible sequences of N events that can occur in each setup. N is the same for the four setups and arbitrarily large. As in [Eberhard1977] and [Eberhard1978], a theory is defined as being "local" if it predicts that, among these possible sequences of events, one can find four sequences (one for each setup) satisfying the following conditions:
(i) The fate of photon a is independent of the value of ##\beta##, i.e., is the same in an event of the sequence corresponding to setup ##(\alpha_1, \beta_1)## as in the event with the same event number k for ##(\alpha_1, \beta_2)##; also same fate for a in ##(\alpha_2, \beta_1)## and ##(\alpha_2, \beta_2)##; this is true for all k's for these carefully selected sequences.
(ii) The fate of photon b is independent of the value of ##\alpha##, i.e., is the same in event k of sequences ##(\alpha_1, \beta_1)## and ##(\alpha_2, \beta_1)##; also same fate for b in sequences ##(\alpha_1, \beta_2)## and ##(\alpha_2, \beta_2)##.
(iii) Among all sets of four sequences that one has been able to find with conditions (i) and (ii) satisfied, there are some for which all averages and correlations differ from the expectation values predicted by the theory by less than, let us say, ten standard deviations.
These conditions are fulfilled by a deterministic local hidden-variable theory, i.e., one where the fate of photon a does not depend on ##\beta## and the fate of b does not depend on ##\alpha##. For such a theory, these four sequences could be just four of the most common sequences of events generated by the same values of the hidden variables in the different setups. Conditions (i)—(iii) are also fulfilled by probabilistic local theories, which assign probabilities to various outcomes in each of the four setups and assume no "influence" of the angle ##\beta## on what happens to a and no "influence" of ##\alpha## on b. With such theories, one can generate sequences of events having properties (i) and (ii) by Monte Carlo, using an algorithm that decides the fate of a without using the value of ##\beta## and, for b, without using the value of ##\alpha##. If the same random numbers are used for the four different setups, the sequences of events will automatically have properties (i) and (ii), and the vast majority of them will have property (iii).
Let us follow an argument first used in Ref. [Stapp1971]. When four sequences are found satisfying conditions (i) and (ii), the four events with the same event number k in the four different sequences will be called "conjugate events". Because of condition (i), two conjugate events in setups ##(\alpha_1, \beta_1)## and ##(\alpha_1, \beta_2)## fall into two boxes on the same row in Table I. The same thing applies for conjugate events in setups ##(\alpha_2, \beta_1)## and ##(\alpha_2, \beta_2)##. Because of (ii), conjugate events for setups ##(\alpha_1, \beta_1)## and ##(\alpha_2, \beta_1)## lie in boxes in the same column; and so do conjugate events for ##(\alpha_1, \beta_2)## and ##(\alpha_2, \beta_2)##. Let us select all the ##n_{oo}(\alpha_1, \beta_1)## events that fall into the box marked with a ##\bullet## in the section of Table I reserved for setup ##(\alpha_1, \beta_1)##. None of these events falls into any other box for setup ##(\alpha_1, \beta_1)##. Because of condition (i), their conjugate events in setup ##(\alpha_1, \beta_2)## fall into boxes on row o. Because of condition (ii), the conjugate events in setup ##(\alpha_2, \beta_1)## lie in boxes in column o. Therefore none of the boxes marked with a ##*## contains any of the events of this sample or any of their conjugates.
Now, from that sample, let us remove events with conjugates falling in one of the boxes marked with a ##\otimes## in setup ##(\alpha_2, \beta_1)##. The number of events subtracted is smaller than or equal to the total number ##n_{uo}(\alpha_2, \beta_1)## + ##n_{eo}(\alpha_1, \beta_1)## of events of all categories contained in those two boxes. Therefore the remaining sample contains ##n_{oo}(\alpha_1, \beta_1) — n_{uo}(\alpha_2, \beta_1) — n_{eo}(\alpha_2, \beta_1)## events or more. None of the events in the remaining sample has a conjugate falling in a box on rows u or e in setup ##(\alpha_2, \beta_1)##; thus, because of condition (i), none falls in setup ##(\alpha_2, \beta_2)## either. None of the conjugate events falls in a box marked with an ##\times## .
Let us further restrict the sample by removing events with conjugates in sequence ##(\alpha_1, \beta_2)## falling in boxes marked with a ##\oplus## in Table I. Using the same argument as in the preceding paragraph, the number of events left must be more than or equal to
##n_{oo}(\alpha_1, \beta_1) — n_{uo}(\alpha_2, \beta_1) — n_{eo}(\alpha_2, \beta_1) — n_{ou}(\alpha_1, \beta_2) — n_{oe}(\alpha_1, \beta_2)##
where ##n_{ou}(\alpha_1, \beta_2) + n_{oe}(\alpha_1, \beta_2)## is the total number of events of all categories falling into the boxes marked with a ##\oplus##. None of the events in that restricted sample falls in column u and e in setup ##(\alpha_1, \beta_2)##; therefore, because of condition (ii), none falls in setup ##(\alpha_2, \beta_2)## either; therefore, none falls in any box marked with a ##+## .
All events belonging to the latter sample must have conjugates in sequence ##(\alpha_2, \beta_2)## falling into the only remaining box for that setup, i.e., box (o,o). That is possible only if that most restricted sample contains a number of events less than or equal to the total number ##n_{oo}(\alpha_2, \beta_2)## of events of all categories in that box. Thus conditions (i) and (ii) can be satisfied by our four sequences only if
##n_{oo}(\alpha_1, \beta_1) — n_{uo}(\alpha_2, \beta_1) — n_{eo}(\alpha_2, \beta_1) — n_{ou}(\alpha_1, \beta_2) — n_{oe}(\alpha_1, \beta_2) \leq n_{oo}(\alpha_2, \beta_2)## (12)
i.e.,
##\mathit{J_B} = n_{oe}(\alpha_1, \beta_2) + n_{ou}(\alpha_1, \beta_2) + n_{eo}(\alpha_2, \beta_1) + n_{uo}(\alpha_2, \beta_1) + n_{oo}(\alpha_2, \beta_2) - n_{oo}(\alpha_1, \beta_1) ## (13)
For condition (iii) to be true no matter how large the number of events N is, inequality (13) also has to apply to the expectation values of these numbers. It is a form of the Bell inequality, which Eqs. (6)—(9) make equivalent to inequality (4) of Ref. [CH1974].