Seems you've found the answer. I know you've used Gravity Simulator before. If it's still installed on your computer, you can get the answer from there too, but it might take a while. Start with any simulation that uses JPL's numbers to produce an accurate solar system, using Earth/Moon barycenter, rather than Earth and Moon as separate objects. In the File menu, have it output a file containing the orbital elements of Earth and any planet. Run the simulation at a slow time step (64 seconds or less). If the program is left to run in the background for a few days, you might be able to get close to 1 million years of sim. Then use Excel to plot the data file. You'll find your eccentricity plot for Earth looks very similar to the one in your second link, with 100,000 year cycles on top of a larger 400,000 year cycle. Here's an example, but this one runs forwards in time, not in reverse as the one in your link.
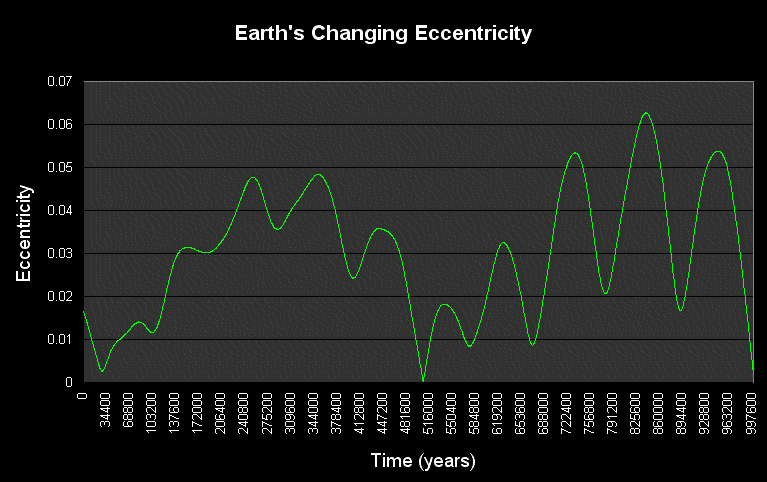
If you did run Gravity Simulator backwards to recreate the graph you linked to, you'd probably find that the graph it creates is in good agreement with their graph up to a point. Beyond that, they diverge. The solar system is chaotic enough that going too far into the future with either method (their graph probably uses analytic perturbation theory) will give untrustable results. The overall patterns of 100,000 and 400,000 year cycles will remain, but the graphs will get out of phase.
Another interesting thing to try is to see how eccentricity changes insolation, the amount of solar flux received by Earth. For this, delete Earth, and recreate it with its minumum eccentricity. Run the sim for 1 year, saving a data file of its position vector once a day. Then in Excel, turn the position vector into a distance from the sun. Make a column for insolation (Solar Luminosity *4 * pi * distance^2), once for each day, and take the average of all 365 days. You'll find that planets in more eccentric orbits receive more insolation than less eccentric orbits. Our orbit is currently getting rounder, meaning we're receiving less sunlight per year. But the difference is not very significant. The big reason that changing eccentricity affects climate is that the Northern and Southern hemispheres are not equally efficient at absorbing/reflecting sunlight. With the Earth's current eccentricity, it receives about 7% more insolation at perihelion than at apihelion. Perihelion currently coinsides with Southern Hemisphere summer.
It's also neat to see how the other orbital elements change with time, for Earth and the other planets. Deleting Jupiter and comparing results shows that Jupiter is the main contributor to the oscillating orbital elements of all the planets.
It's strange to think that the Earth's orbit has inclination, as Earth's orbit defines the plane. But the plane is only defined for one instant (currently we use Jan 1, 2000 at 12 noon GMT). The Earth's inclination has since drifted a small bit from inc=0.