Does Electric Field Depend Solely on Internal Charges?

[musicfairy]

Can someone please check my answers and explain if I get any wrong?

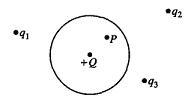
1. A point charge +Q is inside an uncharged conducting spherical shell that in turn is near several isolated point charges, as shown above. The electric field at point P inside the shell depends on the magnitude of
(A) Q only
(B) the charge distribution on the sphere only
(C) Q and the charge distribution on the sphere
(D) all of the point charges
(E) all of the point charges and the charge distribution on the sphere

Is it E? Electric field doesn't only depend on what's in the enclosed surface, does it?

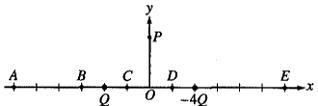
Particles of charge Q and -4Q are located on the x-axis as shown in the figure above. Assume the particles are isolated from all other charges.

2. Which of the following describes the direction of the electric field at point P?
(A) + x
(B) + y
(C) - y
(D) Components in both the - x and + y directions
(E) Components in both the + x and - y directions

E, it's attracted to -4Q, so it's direction would be toward -4Q, or -y and +x

3. At which of the labeled points on the x-axis is the electric field zero? (same picture as above)

(A) A
(B) B
(C) C
(D) D
(E) E



I should put it closer to the charge with a lesser magnitude so I'm guessing B?

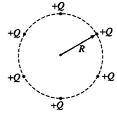
4. What is the magnitude of the resultant electric field at the center of the circle?

Without even looking all the answers, I'll have to say that E = 0. Is this correct?


5. A uniform spherical charge distribution has radius R. Which of the following is true of the electric field strength due to this charge distribution at a distance r from the center of the charge?
(A) It is greatest when r = 0.
(B) It is greatest when r = R/2.
(C) It is directly proportional to r when r > R.
(D) It is directly proportional to r when r < R.
(E) It is directly proportional to r².

Is it C?

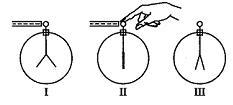
When a negatively charged rod is brought near, but does not touch, the initially uncharged electroscope shown above, the leaves spring apart (I). When the electroscope is then touched with a finger, the leaves collapse (II). When next the finger and finally the rod are removed, the leaves spring apart a second time (III). The charge on the leaves is
(A) positive in both I and III
(B) negative in both I and III
(C) positive in I, negative in III
(D) negative in I, positive in III
(E) impossible to determine in either I or III



Is it A?



Please help.

 

[CompuChip]

Is it E? Electric field doesn't only depend on what's in the enclosed surface, does it?

Doesn't it? What does Gauss's law say?

When you put some charges around (or inside) a conducting sphere, what happens to the charge carriers (electrons) on the surface of the sphere?

E, it's attracted to -4Q, so it's direction would be toward -4Q, or -y and +x

Yes, but it is also repelled by the Q charge, which will contribute something with positive x AND positive y components to the electric field. So I'd say you have to argue a bit more precise.

3. At which of the labeled points on the x-axis is the electric field zero? (same picture as above)
I should put it closer to the charge with a lesser magnitude so I'm guessing B?

When in doubt, calculate.
I suppose you know the expression for the electric field, and by symmetry it is easy to see that the y-component is zero anyway. So you just need to consider the x-component for points on the x-axis; suppose the one charge is at x = 1 and the other at x = -1... what is the x-component of the total E-field as a function of x?

4. What is the magnitude of the resultant electric field at the center of the circle?

Without even looking all the answers, I'll have to say that E = 0. Is this correct?

Why?

5. A uniform spherical charge distribution has radius R. Which of the following is true of the electric field strength due to this charge distribution at a distance r from the center of the charge?

You should be able to find this in any electromagnetism textbook... what do you know about the electric field outside a uniform spherical charge distribution? (Actually, IIRC it goes for any spherical charge distribution). What do you know about the field (or potential) inside it?

When a negatively charged rod is brought near, but does not touch, the initially uncharged electroscope shown above, the leaves spring apart (I). When the electroscope is then touched with a finger, the leaves collapse (II). When next the finger and finally the rod are removed, the leaves spring apart a second time (III). The charge on the leaves is ...

So it must be A or B, because the leaves spring apart so the charges are equal on both. The question is then to determine whether the charge is positive or negative... you say it is positive. Can you explain why?