- #1
Peter Martin
- 32
- 2
Does the “space twin” benefit from length contraction as well as time dilation?
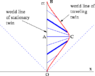
In Einstein’s thought experiment, let one of twins travel to a galaxy known to be 10 light years from Earth at a speed of sixty percent of light speed (0.6c). Were it not for time dilation the one-way trip would take him 10 light years divided by 0.6 light years per year, or 16.7 years.
But because, for him, time passes at only 80% of time on Earth, he experiences the passage of only 13.3 years. Thus on return, he has aged 26.6 years while his “Earth twin” has aged 33.3 years.
But for the space twin, the galaxy is only 8 light years distant due to length contraction. So his round-trip travel time is only 21.3 years.
Does he benefit from both time dilation and length contraction?
In Einstein’s thought experiment, let one of twins travel to a galaxy known to be 10 light years from Earth at a speed of sixty percent of light speed (0.6c). Were it not for time dilation the one-way trip would take him 10 light years divided by 0.6 light years per year, or 16.7 years.
But because, for him, time passes at only 80% of time on Earth, he experiences the passage of only 13.3 years. Thus on return, he has aged 26.6 years while his “Earth twin” has aged 33.3 years.
But for the space twin, the galaxy is only 8 light years distant due to length contraction. So his round-trip travel time is only 21.3 years.
Does he benefit from both time dilation and length contraction?