Double integral with polar coordinates

[Amaelle]

Homework Statement

look at the image

Relevant Equations

polar coordinates

Greetings!
I have the following integral

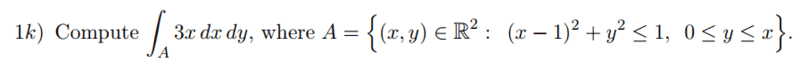
and here is the solution of the book (which I understand perfectly)

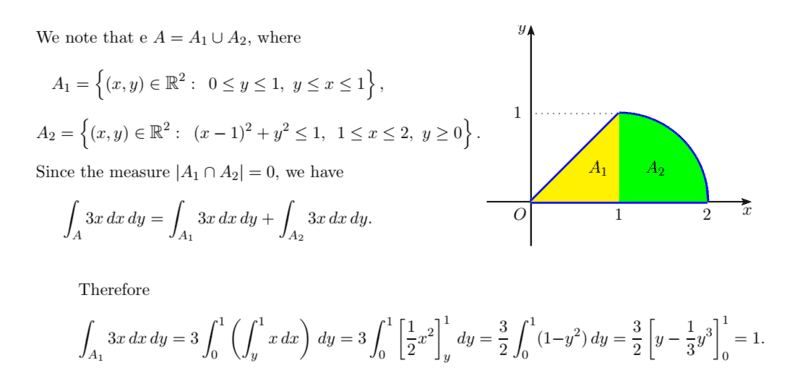
I have an altenative method I want to apply that does not seems to gives me the final resultMy method

which doesn't give me the final results!
where is my mistake?
thank you!

 

[ergospherical]

You can write \begin{align*}
I &= \int_0^{\pi/4} \int_0^{\sqrt{2+2\cos{2\theta}}} 3r^2 dr d\theta \\
&= \int_0^{\pi/4} \cos{\theta} \left( 2+2\cos{2\theta}\right)^{3/2} d\theta \\
&= 8 \int_0^{\pi/4} \cos^4{\theta} d\theta
\end{align*}then\begin{align*}
\int \cos^4{x} dx &=\int \dfrac{(e^{ix} + e^{-ix})^4}{16} dx \\
&= \int \left(\dfrac{e^{4ix} + e^{-4ix} + 4e^{2ix} + 4e^{-2ix} + 6}{16} \right) dx \\
&= \int \left( \dfrac{1}{8} \cos{4x} + \dfrac{1}{2} \cos{2x} + \dfrac{3}{8} \right) dx \\
&= \dfrac{1}{32} \sin{4x} + \dfrac{1}{4} \sin{2x} + \dfrac{3}{8} x \bigg{|}_{0}^{\pi/4} \\
&= \dfrac{1}{4} + \dfrac{3\pi}{32}
\end{align*}

 

[Amaelle]

You can write
\begin{align*}
I &= \int_0^{\pi/4} \int_0^{\sqrt{2+2\cos{2\theta}}} 3r^2 dr d\theta \\
&= \int_0^{\pi/4} \cos{\theta} \left( 2+2\cos{2\theta}\right)^{3/2} d\theta \\
&= 8 \int_0^{\pi/4} \cos^4{\theta} d\theta
\end{align*}
then
\begin{align*}
\int \cos^4{x} dx &=\int \dfrac{(e^{ix} + e^{-ix})^4}{16} dx \\
&= \int \left(\dfrac{e^{4ix} + e^{-4ix} + 4e^{2ix} + 4e^{-2ix} + 6}{16} \right) dx \\
&= \int \left( \dfrac{1}{8} \cos{4x} + \dfrac{1}{2} \cos{2x} + \dfrac{3}{8} \right) dx \\
&= \dfrac{1}{32} \sin{4x} + \dfrac{1}{4} \sin{2x} + \dfrac{3}{8} x \bigg{|}_{0}^{\pi/4} \\
&= \dfrac{1}{4} + \dfrac{3\pi}{32}
\end{align*}

thank you but your code is not readable

 

[ergospherical]

thank you but your code is not readable

Yeah I don't know why that's happening, the LaTeX is fine and works when I run it on Overleaf.

 

[Amaelle]

@ergospherical thank you very much!
indeed my approach was correct, I only messed up with the calculation when I was trying to integrate 8*cos^5 instead of 8*cos^4
thank you again!

 

[berkeman]

Yeah I don't know why that's happening, the LaTeX is fine and works when I run it on Overleaf

It looks like you had no space before \begin and left off the ## delimiters at start/end. I fixed it but you deleted it as I was fixing it...