Drawing a Sketch of a Function with Specified Properties

[xX-Cyanide-Xx]

This is another question that is impossible for me to complete.i don't even know whereto start.
PLLLease help me.

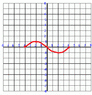
Draw a sketch of a function with the following properties:

a) The gradient is negative where -2 < x < 2
b) The gradient is positive where x < -2 and where x > 2
c) The gradient of the function is zero at (-2, 1) and (2, -1)
d) The zeros of the function are (-4, 0); (0, 0); and (4, 0)

 

[Mentallic]

Why is this impossible to complete? How can you not possibly know where to start? If you know which way the negative and positive gradients slope, and what zero gradient looks like, and what a zero of the function is, this question is really really easy...
If you don't know what all those things are, you need to revise.

 

[xX-Cyanide-Xx]

Why is this impossible to complete? How can you not possibly know where to start? If you know which way the negative and positive gradients slope, and what zero gradient looks like, and what a zero of the function is, this question is really really easy...
If you don't know what all those things are, you need to revise.

Yea, i am really bad at this. i hav been trying this question for hours. can u show me an example or somthing?

 

[Mentallic]

Seriously? Not bragging here but it took me just as long to draw the graph as it did to draw the axis and such.
What are you really bad at? Look at dot points 3 and 4 and they should give you the kick start you need. Draw dots on your graph or something to indicate that those points lie on your function. Since it says at x=\pm2 the gradient is zero, draw a short horizontal line through those points to indicate this. Draw a line anywhere between x=-2 and x=2 that is slanting with a negative gradient to indicate which way the graph is going.

But even if you just labelled all the points that you know, it's pretty much as easy as connect-the-dots.

 

[xX-Cyanide-Xx]

ive had a closer . look, but I am still a little confused about hoe to draw the graph. how do i know wat shape is it? like is it cubic, or Quadratic.. so on.

I'm really sorry for being annoying but I am a very slow learner. but i appreciate your help.

 

[Mentallic]

Look at the last dot point again.

 

[xX-Cyanide-Xx]

i had a look at them, i even tried graphing them, but it just makes a straight line. you said that u drew a graph before. could you please show me that graph and tell me which points are which?

 

[Mentallic]

You tried using a graphics calculator to see what it comes up with when you enter in the 3 zeroes (-4, 0), (0, 0), and (4, 0) ?

What do you mean by "tell me which points are which"? Why don't you put that graphics calculator down for a second, include the info from dot point 3 on your graph (which you should have drawn up on paper by now) and then, even though the answer should be clear from this point, look at dot points 1 and 2 for clarification.

 

[xX-Cyanide-Xx]

i had another look. should the graph look like this? the picture is in the attachment. i made it in paint.

 

[xX-Cyanide-Xx]

that graph is just the points from part 3 and 4 of the question. then i connected the dots.

is this correct?

 

[Mentallic]

I can't see attachments until they're approved. Does the graph look like a quadratic, or a cubic, or a quartic etc.?

 

[Mentallic]

that graph is just the points from part 3 and 4 of the question. then i connected the dots.

is this correct?

As long as it's a smooth curve, with no sharp turns or anything, then yes it's correct.

 

[xX-Cyanide-Xx]

yay,thats wat i did, and it came out to be a cubic graph. so that's correct?

can u check later once the attachment is approved just to check and make sure?

ur even better than my maths teacher.

 

[Mentallic]

Yes it's a cubic. This should be very clear by the fact that there are 3 zeroes to this function.
Now, I didn't want to bring this up earlier because it would've made things more complicated without them needing to be, but you might be interested to know that there are no real cubics that can have have the info you provided. It's not possible to make a cubic have zeroes -4,0,4 AND turning points at x=\pm 2.

Also, even though it says that for x>4 and x<-4, the gradient is positive, this doesn't necessarily mean for large positive x, the function becomes very large and for large negative x, the function becomes very largely negative. You can have things like horizontal asymptotes which the function approaches but never reaches, and still have positive gradient.

 

[Mentallic]

Ok, looking at your attachment, I would agree that it's not possible to determine exactly what happens at x>4 and x<-4, but I'd assume that the function is continuous for all x, so you should extend the graph so that it keeps going on like all cubics do. All you have to do is extend the lines at either end on the positive and negative side and put arrows on the end of them to show that it keeps going.

 

[xX-Cyanide-Xx]

but wat do i do for these parts:
a) The gradient is negative where -2 < x < 2
b) The gradient is positive where x < -2 and where x > 2

 

[Mentallic]

Umm... Do you know which way a line with positive gradient slopes, and which way a negative gradient line slopes? Well all you do is make sure your curve is sloping the correct way in those regions.

 

[xX-Cyanide-Xx]

I kinda get where ur at, it would be easier if i new wat the question ment in more detail. so wat does this symbol mean in this question: <. and wat does the question actually ask.(explain every detail anout wat this,-2 < x < 2. and this means, x < -2 and where x > 2.)

 

[Mentallic]

You don't know what < and > mean? This is basic stuff learned in primary school. x<-2 reads "x is less than -2" and -2<x<2 reads "-2 is less than x is less than 2" so this is saying all values of x between -2 and 2.

 

[Redbelly98]

but wat do i do for these parts:
a) The gradient is negative where -2 < x < 2
b) The gradient is positive where x < -2 and where x > 2

(a) Check the slope (gradient) of your graph between -2 < x < 2. Does the slope appear to be positive or negative there?

 

[xX-Cyanide-Xx]

The line is negative between -2 < x < 2.
and th line is positive where x < -2 and where x > 2.

is this correct?

 

[Redbelly98]

Yes. Therefore your graph is consistent with (a) and (b).

 

[xX-Cyanide-Xx]

thanks u guys. couldn't have done it without u.
i also have another post with different questions if u want to help.
THANKS...:)