blue-steel
- 6
- 0
Hi all,
(see the attached images)
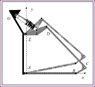
working on a dynamics project about the suspension system in a bike, we have been given a 4 bar linkage - dynamic system, and I am trying to find the velocity of POINT C and POINT F, but given in terms of the angular velocity of bar AB in the STATIC POSITION the solid grey position, the other 'shadow' image is the linkage at it's deflected image,
the 2 images attached show a diagram of the system, Point C represents the centre of the back wheel, all black circles are pivot points, the second gives the coordinates of the points in the two positions
what I am workin on so far is the relative velocity relationship, Vc = Vb + Vc/b to find Vc, only problem is this (ultimately) involves omega_BC when the final value for Vc should only involve omega_AB
should look something like this
Vc = somenumber.omegaAB.i + somenumber.omegaAB.j
anyone familiar with similar problem or have any advice on how to go about it would greatly appreciate it
Cheers
blue steel
(see the attached images)
working on a dynamics project about the suspension system in a bike, we have been given a 4 bar linkage - dynamic system, and I am trying to find the velocity of POINT C and POINT F, but given in terms of the angular velocity of bar AB in the STATIC POSITION the solid grey position, the other 'shadow' image is the linkage at it's deflected image,
the 2 images attached show a diagram of the system, Point C represents the centre of the back wheel, all black circles are pivot points, the second gives the coordinates of the points in the two positions
what I am workin on so far is the relative velocity relationship, Vc = Vb + Vc/b to find Vc, only problem is this (ultimately) involves omega_BC when the final value for Vc should only involve omega_AB
should look something like this
Vc = somenumber.omegaAB.i + somenumber.omegaAB.j
anyone familiar with similar problem or have any advice on how to go about it would greatly appreciate it
Cheers
blue steel