Dynamics of a particle moving in a straight line question

[synkk]

A car of mass 900 kg is towing a trailer of mass 300 kg along a straight horizontal road. The car and the trailer are connected by a light inextensible tow-bar and when the speed of the car is 20m s−1the brakes are applied. This produces a braking force of 2400 N. Find

a the deceleration of the car,

b the magnitude of the force in the tow-bar,

c the distance traveled by the car before it stops.

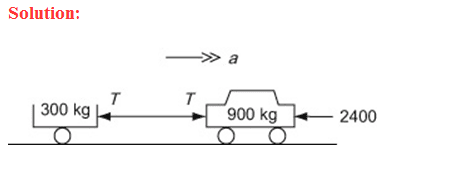
Could anyone explain to me why the tension of the car and trailer is against them? Is it because the car is decelerating?

 

[tiny-tim]

hi synkk!

ould anyone explain to me why the tension of the car and trailer is against them? Is it because the car is decelerating?

yes

T is actually compression rather than tension (it pushes outward)

if the towbar was a rope, then the car would decelerate but the trailer would carry on at the original speed, so they would get closer

since that isn't happening, the towbar must be keeping them apart, so the force in it must be compression (outward)

 

[synkk]

hi synkk!


yes

T is actually compression rather than tension (it pushes outward)

if the towbar was a rope, then the car would decelerate but the trailer would carry on at the original speed, so they would get closer

since that isn't happening, the towbar must be keeping them apart, so the force in it must be compression (outward)

fast reply, thanks.