stunner5000pt
- 1,443
- 4
This isn't so much an astronomy question as one would think
A perfectly black satellite is in orbit around the Earth at a height of 2000 km
What solid angle does the Earth subtend when viewed from teh satellite?
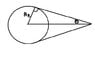
\cos \theta = \frac{6370km}{8370km}
WEll if we look at hte diagram the angle theta is 40.4 degrees or 0.705 radians
we want the solid angle which is defined as
\Omega = \int_{0}^{2 \pi} \int_{0}^{0.705} \sin \theta' d \theta' d \phi
is this fine?
A perfectly black satellite is in orbit around the Earth at a height of 2000 km
What solid angle does the Earth subtend when viewed from teh satellite?
\cos \theta = \frac{6370km}{8370km}
WEll if we look at hte diagram the angle theta is 40.4 degrees or 0.705 radians
we want the solid angle which is defined as
\Omega = \int_{0}^{2 \pi} \int_{0}^{0.705} \sin \theta' d \theta' d \phi
is this fine?
Attachments
Last edited: