- #1
nezednemo
- 8
- 3
- TL;DR Summary
- How much weight will it take to destabilize a table at the furthest most offset edge?
Hello,
a little about me: I’m a self trained craftsmen who has a deep hunger for knowledge. I have no formal training in physics or engineering. There are some principles I‘d like to understand better to improve my workflow. Please forgive any terminology faux pas, part of the issue I have in searching for these answers is I don’t have all the vocabulary down.
(1) I’d like to know how to calculate the force necessary to tip a cantilevered object like the table below.
(2) I’d like to have a better Understanding of how to calculate the combined center of mass of complex objects.
(3) I’d like to know if there are any rule of thumbs for angles of offsets. Obvious ≥ 90° is most stable, but is there an engineering principle that I could use to make. Faster calculations when designing products like this?
Thank you for your help
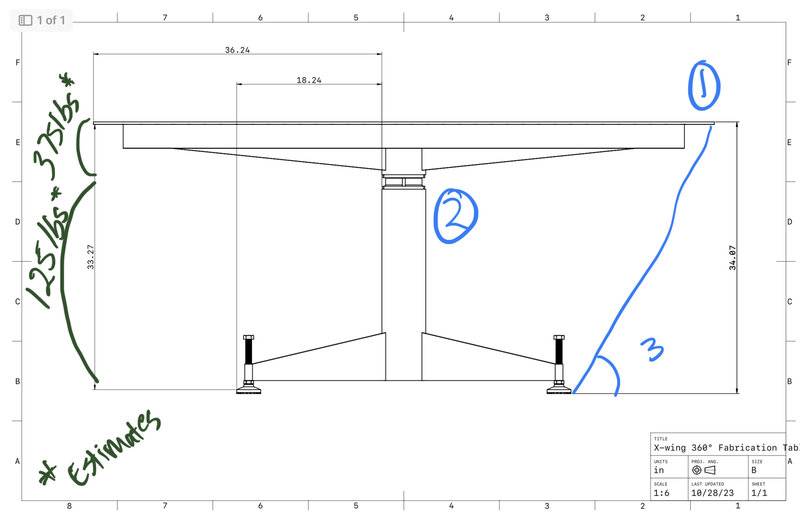
a little about me: I’m a self trained craftsmen who has a deep hunger for knowledge. I have no formal training in physics or engineering. There are some principles I‘d like to understand better to improve my workflow. Please forgive any terminology faux pas, part of the issue I have in searching for these answers is I don’t have all the vocabulary down.
(1) I’d like to know how to calculate the force necessary to tip a cantilevered object like the table below.
(2) I’d like to have a better Understanding of how to calculate the combined center of mass of complex objects.
(3) I’d like to know if there are any rule of thumbs for angles of offsets. Obvious ≥ 90° is most stable, but is there an engineering principle that I could use to make. Faster calculations when designing products like this?
Thank you for your help