Effective Current Impedance Calculation without Inductive Coupling

[radicaled]

The exercise goes like this:
- Obtain the impedance
- Current effective without inductive coupling

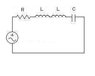
Data:
v(t) = 100 sin(1000t + π/3)
R = 1kΩ
L1 = L2 = 1H
C= 1μC

Resolution:
$Z = \sqrt{R^2 + (Xl - Xc)^2}$
$Z = \sqrt{1000^2 + (1000.2 - \frac{1}{1000 1x10^{-6}})^2}$
$Z = 1414,21$Ω

Now, what is the inductive coupling

 

[gneill]

Without a circuit diagram the question is ambiguous. Can you provide a circuit diagram and the original problem statement?

 

[radicaled]

Ok, I have attached the circuit.
As for the problem statement its the same. I may rephrase, because I have to translate it
- Obtain the impedance
- The effective current without inductive coupling

 

[gneill]

You've calculated a magnitude for the impedance, but the impedance itself will be a complex value (real and imaginary parts). You can find the magnitude of the current that flows by treating the impedance magnitude as though it were a simple resistance. Note that this will not provide current phase information (with respect to the applied voltage, which as you should note, has its own specified phase). For the phase information you will have to use the complex impedance and perform the calculation using complex arithmetic.

Inductive coupling is the interaction of inductors that share a mutual magnetic field; current in one inductor induces a current in the other, and vice-versa. Apparently you're asked to ignore such a coupling in this problem.