Einsteins field equations us what type of index notation?

[oddjobmj]

I know that the metric tensor itself utilizes Einstein summation notation but the field equations have a tensor form so the μ and ν symbols represent tensor information.

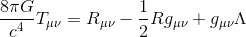
I'm trying to wrap my head around how Einstein used summation notation to simplify the above field equations but it seems to be more of a tensor notation than anything. Is it used here at all?

Edit: Ah, too early to spell 'use' correctly apparently...

 

[Orodruin]

A tensor by itself does not utilise the summation convention. The summation convention is used to simplify contraction of indices. There is no such contraction in the Einstein field equations and both $\mu$ and $\nu$ are free indices.

 

[oddjobmj]

Thank you! It's not even wrapped into the components in anyway that might not be immediately visible?

 

[Orodruin]

Well, the Ricci tensor and Ricci scalar are simply contractions of the Riemann curvature tensor, so implicitly there are some contractions where you could use the summation convention, but in the end these are already done.

 

[oddjobmj]

Ah, the way the metric tensor was explained to me was with a triangle that might be in curved space which you are trying to find the hypotenuse of where the following is the metric tensor:

Which comes from: