- #1
Nihuepana
- 4
- 0
[SOLVED] Elastic and gravitational potential energy
First off, long time lurker here on his first post. Your forum seems absolutely brilliant, so I hope you can help me :)
A box on an elastic string is dropped down an incline and proceeds to slide the distance L before being pulled back by the string and stopping at the distance L/2. At the starting point the string is slack. Find the coefficient of friction and the spring constant.
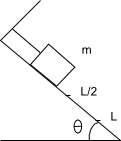
Known data:
U_{{{\it el2}}}=1/2\,k{x}^{2}
U_{{{\it grav}}}=mgy
y=\sin \left( \theta \right) L
W_{{{\it res}}}=-mg\cos \left( \theta \right) \mu\,x
{\it K1}+U_{{{\it grav1}}}+W_{{{\it res12}}}={\it K2}+U_{{{\it grav2}}<br /> }+U_{{{\it el2}}}
Right, so I've basically just changed x to L plugged in my attributes into {\it K1}+U_{{{\it grav1}}}+W_{{{\it res12}}}={\it K2}+U_{{{\it grav2}}<br /> }+U_{{{\it el2}}} and solved for my variables. I did first for when the box goes from point 1 to point 2, then 2 to 3 and finally 1 to 3. All three equations give me the same answer.
k:
2\,{\frac {mg \left( \sin \left( \theta \right) -\cos \left( \theta<br /> \right) \mu \right) }{L}}
mu:
{\frac {-2\,mg\sin \left( \theta \right) +kL}{mg\cos \left( \theta<br /> \right) }}
What I don't understand is why the problem is formulated as it is (why give me the information that it springs back to L/2, if I don't need it to find the constants).
Also, I was hoping that it would be possible to get equations for the constants where the unknowns doesn't figure, i.e. an equation for the spring coefficient that doesn't have mu in it and vice versa.
I've tried with all the algebra I could think of, but nothing seems to work - is there anyone who can point me to what I'm missing?
Thanks.
Simon
First off, long time lurker here on his first post. Your forum seems absolutely brilliant, so I hope you can help me :)
Homework Statement
A box on an elastic string is dropped down an incline and proceeds to slide the distance L before being pulled back by the string and stopping at the distance L/2. At the starting point the string is slack. Find the coefficient of friction and the spring constant.
Known data:
- Distance, L
- Angle of incline, Theta
- Mass of box, m
Homework Equations
U_{{{\it el2}}}=1/2\,k{x}^{2}
U_{{{\it grav}}}=mgy
y=\sin \left( \theta \right) L
W_{{{\it res}}}=-mg\cos \left( \theta \right) \mu\,x
{\it K1}+U_{{{\it grav1}}}+W_{{{\it res12}}}={\it K2}+U_{{{\it grav2}}<br /> }+U_{{{\it el2}}}
The Attempt at a Solution
Right, so I've basically just changed x to L plugged in my attributes into {\it K1}+U_{{{\it grav1}}}+W_{{{\it res12}}}={\it K2}+U_{{{\it grav2}}<br /> }+U_{{{\it el2}}} and solved for my variables. I did first for when the box goes from point 1 to point 2, then 2 to 3 and finally 1 to 3. All three equations give me the same answer.
k:
2\,{\frac {mg \left( \sin \left( \theta \right) -\cos \left( \theta<br /> \right) \mu \right) }{L}}
mu:
{\frac {-2\,mg\sin \left( \theta \right) +kL}{mg\cos \left( \theta<br /> \right) }}
What I don't understand is why the problem is formulated as it is (why give me the information that it springs back to L/2, if I don't need it to find the constants).
Also, I was hoping that it would be possible to get equations for the constants where the unknowns doesn't figure, i.e. an equation for the spring coefficient that doesn't have mu in it and vice versa.
I've tried with all the algebra I could think of, but nothing seems to work - is there anyone who can point me to what I'm missing?
Thanks.
Simon
Last edited: