Elastic collision and angle of deflection problem

[Ahmed Farhan]

1.

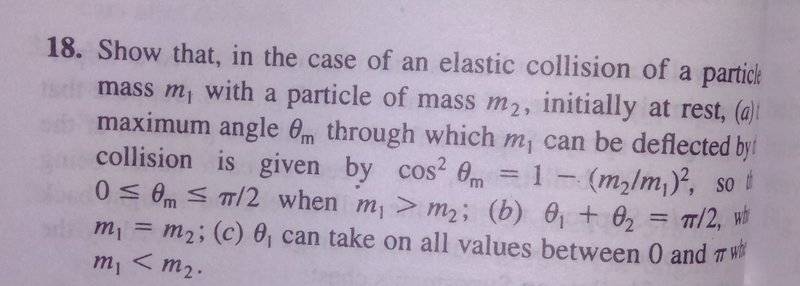2. The equations are the equations of conservation of momentum:
m₁v = m₁v₁cosθ₁ + m₂v₂cosθ₂
0 = m₁v₁sinθ₁ + m₂v₂sinθ₂

3. I tried to solve it using the above equations and also tried using kinetic energy conservation since it's an elastic collision. But I can't work out the algebra. Is there something wrong with the logic? I'm completely lost on this one. Someone please solve this for me.

 

[kuruman]

The relative sign in the "y" equation must be negative otherwise you cannot get the two to add to zero. The symbols v1 and v2 are speeds, therefore positive.

 

[Ahmed Farhan]

The relative sign in the "y" equation must be negative otherwise you cannot get the two to add to zero. The symbols v1 and v2 are speeds, therefore positive.

Should it matter? The sign can be determined by the value of the angles.

 

[QuantumQuest]

I tried to solve it using the above equations and also tried using kinetic energy conservation since it's an elastic collision. But I can't work out the algebra. Is there something wrong with the logic? I'm completely lost on this one. Someone please solve this for me.

Hi Ahmed Farhan

It will be no good for you to get the solution by someone else. In order to learn Physics you have to solve it yourself. I'll give you some hints on this for (a):
take the conservation of momentum as you did and also the conservation of energy. Solve the system of these equations. Your aim is to get the $cos\theta_{m}$. See how you can continue from there.