- #1
rocapp
- 95
- 0
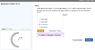
Homework Statement
See the image attached
Homework Equations
Ex = (Kλ/R)*∫3/2ππ/2(cosθ)dθ
The Attempt at a Solution
Ey cancels because there is an equal amount of force in both y directions. For the electric field on the x axis, the above equation can be used.
Given that λ=Q/L
λ=(85x10^-9 C)/(0.1 m)
=8.5x10^-7
R = L/θ
=(0.1 m)/(3/2π - π/2)
=0.03183
E = ((8.85x10^-9)(8.5x10^-7)/0.03183)*pi
= 7.424640507894822×10^-13
This is not correct. Please help! Thanks in advance.