afmower
- 7
- 2
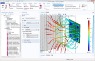
I have a PhD in Molecular Neuroscience but am working on something that requires knowledge of electric field distribution in the brain. I understand that electric field intensity (V/cm) is E=(V1-V2)/d in a theoretical model (between 2 infinite plates, that are parallel and equidistant through a homogeneous medium). In a model where the plates are not parallel and the medium is not homogenous (say the brain for example), field intensity is affected by the distance between the 2 plates, the location and orientation of interfaces between different tissues and the individual dielectric properties of tissues. Here is where I am getting lost...
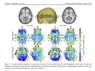
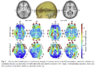
I often see electric field distribution also given in V/cm. How is this possible when intensity and distribution do not seem to be interchangeable or directly proportional according the following:
-Field distribution in serial tissues of increasing resistance: field distribution across the 3 tissues in series is equal regardless of the resistance and intensity is highest in the tissue of highest resistance
-Filed distribution in parallel tissues with different levels of resistance: field distribution is greatest in the tissue with lowest resistance when tissues are parallel and field intensity is equal regardless of resistance
Any insights would be helpful. Thank you in advance.
I often see electric field distribution also given in V/cm. How is this possible when intensity and distribution do not seem to be interchangeable or directly proportional according the following:
-Field distribution in serial tissues of increasing resistance: field distribution across the 3 tissues in series is equal regardless of the resistance and intensity is highest in the tissue of highest resistance
-Filed distribution in parallel tissues with different levels of resistance: field distribution is greatest in the tissue with lowest resistance when tissues are parallel and field intensity is equal regardless of resistance
Any insights would be helpful. Thank you in advance.