- #1
- 350
- 28
Electric field is 0 in the center of a spherical conductor. At a point P (black dot), I do not understand how the electric field cancels and becomes 0. Electric field is in blue.
Electric field is zero in the center of a spherical conductor
Answers and Replies
- #2
anuttarasammyak
Gold Member
- 2,002
- 1,063
Whether the conductor shell hold charge or not and grounded or not, matter.
Last edited:
- #3
- 5,695
- 2,475
Gauss's law and spherical symmetry make it zero. But yes if you try to think in terms of the Coulomb's law (like the blue arrows you draw suggest) it is not so obvious.
The intuitive approach to explain it using Coulomb's law is that the part of the conductor that is closest to the point exerts greater electric field but it is smaller in length than the part of the conductor that is furthest apart and hence exerts smaller electric field. The two electric fields cancel out. It is something like $$L_1D_1-L_2D_2=0$$ where ##L_1##,##L_2## the lengths of the bigger and smaller part and ##D_1## and ##D_2## the influence of the bigger and smaller part. The bigger part has smaller influence and the smaller part has bigger influence. So it is ##L_1>L_2## but ##D_1<D_2##. All these are very intuitive though, if you want a formal treatment of this using coulomb's law you have to do a hard integral to prove that it is zero at any point in the interior of the sphere.
Yes check @Ibix link for a formal treatment. It is for gravitational field but I guess you get it that it is pretty much the same thing, the same inverse square law holds for electric and gravitation field, in one case we call it Newton's law and in the other case Coulomb's law.
The intuitive approach to explain it using Coulomb's law is that the part of the conductor that is closest to the point exerts greater electric field but it is smaller in length than the part of the conductor that is furthest apart and hence exerts smaller electric field. The two electric fields cancel out. It is something like $$L_1D_1-L_2D_2=0$$ where ##L_1##,##L_2## the lengths of the bigger and smaller part and ##D_1## and ##D_2## the influence of the bigger and smaller part. The bigger part has smaller influence and the smaller part has bigger influence. So it is ##L_1>L_2## but ##D_1<D_2##. All these are very intuitive though, if you want a formal treatment of this using coulomb's law you have to do a hard integral to prove that it is zero at any point in the interior of the sphere.
Yes check @Ibix link for a formal treatment. It is for gravitational field but I guess you get it that it is pretty much the same thing, the same inverse square law holds for electric and gravitation field, in one case we call it Newton's law and in the other case Coulomb's law.
Last edited:
- #4
- 10,569
- 11,471
- #5
- 20,004
- 10,653
Two things are very different and OP needs to understand the difference:
- Why the field inside of a spherically symmetric charge/mass distribution is zero. This has nothing to do with being a conductor.
- Why, in a static situation without currents, the field inside a conductor is zero.
I strongly suspect the OP intends the first of those, but then should not write ”conductor” but ”charge distribution” or similar.
- Why the field inside of a spherically symmetric charge/mass distribution is zero. This has nothing to do with being a conductor.
- Why, in a static situation without currents, the field inside a conductor is zero.
I strongly suspect the OP intends the first of those, but then should not write ”conductor” but ”charge distribution” or similar.
- #6
- 20,004
- 10,653
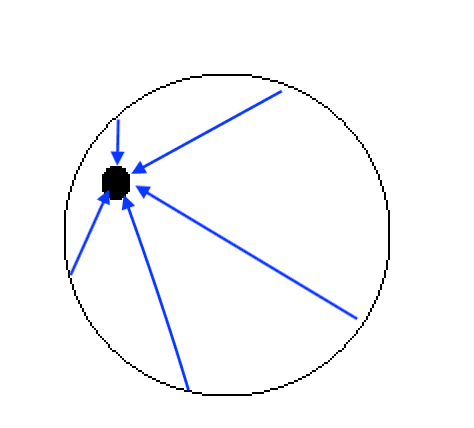
Apart from what has been said already, this does not accurately describe the electric field, but the displacement from the shell to the point. The strength of the field is proportional to the inverse of the square of the displacement.
- #7
- 5,695
- 2,475
Not sure how exactly you mean it here, but the field inside a spherically symmetric distribution is not necessarily zero it is just that to the field contributes only the part of the distribution that has radius smaller than the radius of the point.
I think the OP means a spherical shell of uniform distribution. Yes it doesn't have to be conductor as long as the distribution is uniform.
- #8
- 20,004
- 10,653
That sounds like the definition of the point being ”outside”.
That is my first reading too (spherically symmetric- not uniform), but at least one person has made the other interpretation, see #2.
- #9
- 5,695
- 2,475
It is not adequate just to be inside for the field to be zero, the "inside" has to be empty space too in order to be zero.
I mean for example the field below the Earth surface is not zero, it just contribute to it only the smaller sphere of mass of radius R where R the radius of the point.
- #10
- 22,767
- 13,695
Why should the field inside a spherically symmetric charge distribution be zero?
Just take a homogeneously charged sphere with ##\rho=\text{const}## for ##r<a## (with ##a## the radius of the sphere with center in the origin of our reference frame). It's clear that the electric field is radial everywhere, i.e.,
$$\vec{E}(\vec{r})=E_r(r) \vec{e}_r.$$
With Gauss's Law applied to a sphere of radius ##r## you get
$$4\pi r^2 E_r(r)=\frac{4 \pi}{3 \epsilon_0} r^3 \rho_0\; \Rightarrow \; E_r =\frac{\rho_0}{3 \epsilon_0} r \neq 0.$$
If you have a conductor, there cannot be any charge inside, and thus the electric field inside the conductor is 0.
- #11
- 5,695
- 2,475
yes this is what I had in mind. However if we have a hollow spherically symmetric distribution (that is a spherical shell of some thickness) then the field is zero inside the hollow space.
- #12
- 20,004
- 10,653
Then it is impossible to be on the inside of the charge distribution as you cannot have ##r < r_0##, where ##r_0## is the smallest radius for which the charge distribution is non-zero ... except for the quite uninteresting case of ##r = 0## of course ... but there the field is zero by simple symmetry arguments.
- #13
- 5,695
- 2,475
Depends how you mean that "inside" e hehe. In the everyday language when we say for example "inside the box" we mean inside the empty space that is bounded by the box, and not inside the material that makes up the walls of the box.
However I think here inside the distribution means inside the space where ##\rho>0##.
However I think here inside the distribution means inside the space where ##\rho>0##.
Last edited:
- #14
- 20,004
- 10,653
Well, when I first used the word "inside" in this thread I certainly intended the hollow region inside a spherically symmetric charge distribution where ##\rho = 0##.
Last edited:
- #15
- 22,767
- 13,695
Why can't I be "inside" a charge distribution?
- #16
- 5,695
- 2,475
You have to be a transcendental being in order to be inside something without your presence altering that something...
E hehe just joking...
- #17
- #18
- 350
- 28
What do your D's stand for. The electric field of the smaller length is greater than the electric field of the greater length, so there should be a net positive electric field...Not sure how they cancel out.
- #19
- 5,695
- 2,475
First of all my treatment is very intuitive. My D's stand for something like average electric field (generated by ) per unit length of charge density. The average electric field per unit length of the smaller part is greater (than the electric field per unit length of the biggest part) because the smaller part is closer to the point so by the inverse square law generates bigger electric field.
- #20
- 20,004
- 10,653
Your logic is flawed here. If you consider a small solid angle in one direction and the opposite direction, the amount of charge within that solid angle will be smaller for the closer side and larger for the farther side so there is simply more charge on the farther side. This exactly cancels the charges closer giving a larger contribution per unit charge.
- #21
- 350
- 28
I don't understand why the densities D would not be the same...
- #22
- 20,004
- 10,653
It is not about the surface density. It is about the amount of charge per solid angle.
- #23
- 20,004
- 10,653
Here is an illustration I quickly put together using the picture from your OP by adding two red lines:
As you can see, there is a lot more charge between the red lines to the right than to the left, yet this is what represents the opposite direction of the charge between the red lines to the left. This effect is what exactly cancels the closer charges giving more field strength per charge.
As you can see, there is a lot more charge between the red lines to the right than to the left, yet this is what represents the opposite direction of the charge between the red lines to the left. This effect is what exactly cancels the closer charges giving more field strength per charge.
- #24
- 350
- 28
This makes sense for a hollow spherical charge. But is this true for a solid spherical charge?
It seems like for a solid spherical charge, there is more electrical field on the right side.
- #25
jbriggs444
Science Advisor
Homework Helper
- 11,950
- 6,642
Which the shell theorem confirms nicely. The portion of a [spherically symmetric] charge distribution closer to the center than to the test point contributes to the field as if that portion of the total charge were concentrated in the center.
- #26
sophiecentaur
Science Advisor
Gold Member
- 28,019
- 6,407
If you are not exactly in the middle of a "solid (uniform?) spherical charge" then you are outside of some sphere that's 'inside' your position. All those charges will have a net non-zero effect. The effect of each shell, beneath your feet will be that of a single charge at the centre of the sphere, equal to the total charge on the shell. The total field is proportional to the radius of that smaller sphere. It's all down to 'areas' and 'inverse square law', if you want an arm waving explanation.
- #27
- 350
- 28
If charges are uniformly everywhere in a solid sphere, it seems like the purple color cancels the electric field for each other but the right side has extra white electric field.
- #28
- 20,004
- 10,653
There is no charge within the red lines. They have width zero. It is just impossible to draw with width zero.
- #29
- 350
- 28
In a conductor that is a solid sphere without any external electric field, there should be charge uniformly throughout the sphere...I don't understand how charge in a spherical conductor is only on the surface unless induced by a field.
- #30
- 22,767
- 13,695
We should first have a definite description of the charge distribution, before we can make any concrete calculation. As demonstrated already above, for a homogenously charged sphere the electric field is NOT zero inside this sphere.
What can be proven is that, if there is a spherically symmetric charge distribution ##\rho(r)## with ##\rho(r)=0## for ##r<a##, that then ##\vec{E}=0## within this sphere of radius ##a##, because then you have for the potential
$$\phi(\vec{r})=\int_{\mathbb{R}^3} \mathrm{d}^3 r' \frac{\rho(r')}{4 \pi \epsilon_0 |\vec{r}-\vec{r}'|}.$$
Now since ##\rho(r')=0## for ##r'<a##, we have
$$\phi(\vec{r})=\frac{1}{4 \pi \epsilon_0} \int_a^{\infty} \mathrm{d} r' r^{\prime 2} \rho(r') \int_0^{\pi} \mathrm{d} \vartheta' \sin \vartheta' \int_0^{2 \pi} \mathrm{d} \varphi' \frac{1}{\sqrt{r^2+r^{\prime 2}-2 r r' \cos \vartheta'}},$$
where due to symmetry I could choose ##\vec{r}=r \vec{e}_3##, i.e., ##\vec{r} \cdot \vec{r}'=r r'\cos \vartheta##.
Now we do the angle integrations for the case that ##r<a##. The important point is that due to the assumption that ##\rho## vanishes within the sphere of radius ##a## we have ##r' \geq a##:
$$\int_0^{\pi} \mathrm{d} \vartheta' \frac{\sin \vartheta}{\sqrt{r^2 + r^{\prime 2}-2 r r' \cos \vartheta'}}=\int_{-1}^1 \mathrm{d} u \frac{1}{\sqrt{r^2+r^{\prime 2}-2r r' u}}=-\left . \frac{\sqrt{r^2+r^{\prime 2}-2r r' u}}{r r'} \right|_{u=-1}^{u=1}=\frac{1}{rr'} [\sqrt{(r+r')^2}-\sqrt{(r'-r)^2}].$$
Because ##r<r'## the bracket is ##(r+r')-(r'-r)=2r## and thus the said angle-integral is ##2/r'##, such that finally the potential ##\Phi(r)=\text{const}## for ##r<a## and thus ##\vec{E}=-\vec{\nabla} \Phi=0##. QED.
What can be proven is that, if there is a spherically symmetric charge distribution ##\rho(r)## with ##\rho(r)=0## for ##r<a##, that then ##\vec{E}=0## within this sphere of radius ##a##, because then you have for the potential
$$\phi(\vec{r})=\int_{\mathbb{R}^3} \mathrm{d}^3 r' \frac{\rho(r')}{4 \pi \epsilon_0 |\vec{r}-\vec{r}'|}.$$
Now since ##\rho(r')=0## for ##r'<a##, we have
$$\phi(\vec{r})=\frac{1}{4 \pi \epsilon_0} \int_a^{\infty} \mathrm{d} r' r^{\prime 2} \rho(r') \int_0^{\pi} \mathrm{d} \vartheta' \sin \vartheta' \int_0^{2 \pi} \mathrm{d} \varphi' \frac{1}{\sqrt{r^2+r^{\prime 2}-2 r r' \cos \vartheta'}},$$
where due to symmetry I could choose ##\vec{r}=r \vec{e}_3##, i.e., ##\vec{r} \cdot \vec{r}'=r r'\cos \vartheta##.
Now we do the angle integrations for the case that ##r<a##. The important point is that due to the assumption that ##\rho## vanishes within the sphere of radius ##a## we have ##r' \geq a##:
$$\int_0^{\pi} \mathrm{d} \vartheta' \frac{\sin \vartheta}{\sqrt{r^2 + r^{\prime 2}-2 r r' \cos \vartheta'}}=\int_{-1}^1 \mathrm{d} u \frac{1}{\sqrt{r^2+r^{\prime 2}-2r r' u}}=-\left . \frac{\sqrt{r^2+r^{\prime 2}-2r r' u}}{r r'} \right|_{u=-1}^{u=1}=\frac{1}{rr'} [\sqrt{(r+r')^2}-\sqrt{(r'-r)^2}].$$
Because ##r<r'## the bracket is ##(r+r')-(r'-r)=2r## and thus the said angle-integral is ##2/r'##, such that finally the potential ##\Phi(r)=\text{const}## for ##r<a## and thus ##\vec{E}=-\vec{\nabla} \Phi=0##. QED.
- #31
anuttarasammyak
Gold Member
- 2,002
- 1,063
If there are charges under surface, there should be electric field inside the conductor. Free electrons move so that these charges inside disappear.
- #32
- 20,004
- 10,653
Again, there are two lines of argumentation going on here and I become more and more convinced that the OP is mixing them up.
- The field in a hollow central region of a spherically symmetric charge distribution is zero. This is based on the distribution of charges alone. It has nothing to do with the sphere being a conductor.
- The field inside an ideal conductor (or just a conductor without externally applied potential that has reached a stationary state) is zero. This is based on the resistivity of an ideal conductor being zero and has nothing to do with the conductor being a sphere.
Until the OP clarifies that he understands the difference between those two and specifies which is intended, I do not believe we will get any further.
- The field in a hollow central region of a spherically symmetric charge distribution is zero. This is based on the distribution of charges alone. It has nothing to do with the sphere being a conductor.
- The field inside an ideal conductor (or just a conductor without externally applied potential that has reached a stationary state) is zero. This is based on the resistivity of an ideal conductor being zero and has nothing to do with the conductor being a sphere.
Until the OP clarifies that he understands the difference between those two and specifies which is intended, I do not believe we will get any further.
- #33
- 22,767
- 13,695
As shown in my posting above, it's 0 everywhere inside the sphere, if there's a spherically symmetric charge distribution, that is vanishing inside this sphere. It's indeed irrelevant, whether the sphere is a conductor or not.
Last edited:
- #34
- 20,004
- 10,653
Well, this is what I said already in my first post but people did not like the use of ”inside” … I have some doubts whether or not the integration argument will satisfy the OP who seems more intent on qualitative reasoning than actually mathing it out … the confusion regarding what the actual question is does not help either …
- #35
- 16
- 7
Feynman puts it simple, in his "Lectures on Physics", page 5-5:
If the spherical shell is conductive, charge would spread evenly. At any point within the sphere, take for instance "P", the field is due to the contribution of the charges on the sphere. If you think of two opposite cones at "P", each one contributes with the charge that is on the base of that cone (intersecting the sphere). This charge is equal to charge density times area of intersection. The area increases with the square of the distance to "P". The field due to each charge decreases with the square of the distance as well. So they both cancel resulting in a same field contribution for any cone, so if you take cones by pairs (the field of one cone is equal and opposite of the field of the other cone) and integrate over the whole sphere, it yields zero field at any point within the sphere.