guyvsdcsniper
- 264
- 37
- Homework Statement
- In the limit R=0, e.g., when the Oxygen ion is a point charge:
a) Write down the volume charge density (15pts)
b) Draw the electric field lines far away from charges (25pts)
c) Draw the electric field lines near the point charges (25 points)
d) At finite radius R, draw the lines near the charges
- Relevant Equations
- p=q/v
I wanted to post my work so far to see if I am on the right path toward the correct answer so far.
I have attached a ss of the actual problem and my work in the attachments
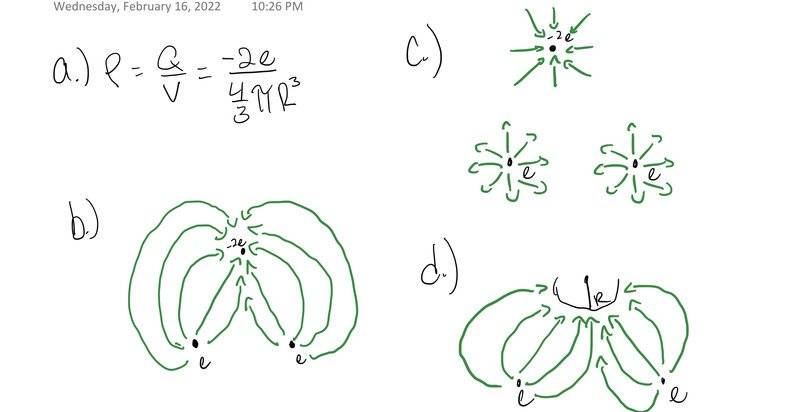

I have attached a ss of the actual problem and my work in the attachments