Abdul Quadeer said:
...
I got q
2= -q
1R/a
I calculated the potential due to q1 and q2 and found them to be equal to -kq
1/R + kq
1/a (assuming that the point B inside the cavity is inside the sphere formed with radius 'p').
Thank you for teaching me about image charges

The q
2 = ‒q
1R/a is correct. (You corrected my sign error.)
Your interpretation isn't quite right.
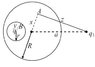
Let's build up a solution using superposition:
A charge of -q
1R/a at x = p, where p = R
2/a and a charge of q
1 at x=a, will produce a potential of zero a distance of R from the origin -- that is the location of the surface of a sphere of radius R centered at the origin.
We could replace a grounded sphere (radius R, center @ origin) with this image charge. The electric potential and the E field would match everywhere beyond a distance of R from the origin, for either configuration.
... but we don't have a grounded sphere.
That brings us to the next step:
Start with a neutral conducting sphere (radius R, center @ origin), bring a charge of q
1 from ∞ to x = a. This sphere is NOT grounded ! We could replace the sphere with our image charge, q
2 = ‒q
1R/a at x = R
2/a , plus a charge of ‒q
2 = +q
1R/a @ the origin, in addition to the charge q
1 @ x = a. But think about it! ... q
2 @ x = p and q
1 @ x = a give us a potential of zero @ a distance of R from the origin, ...
so, simply use a charge of q
1R/a at the origin --- to find what the potential of a neutral conducting sphere of radius R, center @ origin.
However, our sphere has a net charge of q on it's exterior, so to find the potential at it's surface, find the potential @ a distance of R from the origin, due to a charge of q + ‒q
2 = q + q
1R/a all situated at the origin.
This gives the potential of all of the conducting sphere including all the way down to the surface of the cavity in it.