Electric Potential on the axis of a truncated cone

[Rasec98]

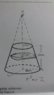
1.Data: We have an truncated cone with a volumentric charge density ρ, and it's uniform. The image show the truncated cone and show some info of the radios.

2. Question. We need to calculate the potential on the vertical axis.

note: adding an image of the problem but it's in spanish, hope someone knows the language...

 

[Delta2]

Hi, @Rasec98

You have to show us some attempt of yours at the solution of the problem, it is against the rules of PF to give you the whole solution.

What is the general integral formula you know that gives the potential V, when the charge density $\rho(\vec{r})$ is known and given by the problem?
I believe you should work with cylindrical coordinates for this problem.
Write down the integral using cylindrical coordinates, and also carefully determine the domain of integration. Then perform the integration.

 

[DrClaude]

This has to be posted in the homework forum, with the homework template filled out.

Posting an image of the question is already stretching the rules, having the question only in Spanish is definitely not acceptable. You have to translate the question to English and write it up in your post.

Thread closed.