Electromagnetism, finding magnetic field strength

[physics604]

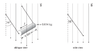
1. A 0.034 kg copper rod is hung by two wires and placed in a constant magnetic field. A current
of 14 A runs through the 0.050 m long copper rod, making it hang at an angle of 34° from the vertical as attached in the diagram.

What is the magnetic field strength holding the copper rod in this position?

A. 27×10^-1 T
B. 32×10^-1 T
C. 39×10^-1 T
D. 48×10^-1 T

Homework Equations

\phi=B×Acosa
F=IlB

The Attempt at a Solution

The thing is, I don't really know where to start.

I know that the rod is at 34° (not perpendicular), so I know the formula \phi=B×Acosa has to be involved somehow. However, I'd only be solving for \phi and I don't know the area so that really isn't very helpful.

I'm also given I and l to find B, and the only equation that looks has these variables is F=IlB. But that would me I need to find force and the other equation is F=QvB and we don't have many variables in that one.

 

[Simon Bridge]

Start by drawing a free body diagram.

 

[physics604]

Okay, I think I got it. So I would solve for the force of tension in the wires and that would be the F. Then I would do B=F/Il.

Just one more question: when I finish solving for F_T, would I have to double it to find F (since there are two wires)?

 

[Simon Bridge]

It's basically a pendulum (use the side view).
If the tension in each wire is T, then the total tension is 2T.
Did you remember the magnetic force and gravity?