The black vegetable
- 22
- 0
Hi
Everyone, I'm trying to justify to myself why
|F(a)| > |F(b)| > |F(c)|
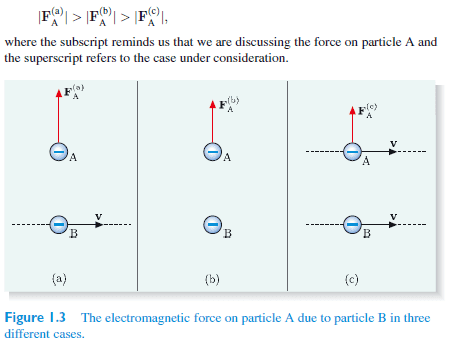
I think I can see why
|F(b)| > |F(c)|
due to special relativity case c observed from
the charges point of view would observe
the charges closer due to lorentz
contraction. As the charge is invariant would
result in a greater force?
However I can't justify to myself why
|F(a)| > |F(b)|
many thanks
Everyone, I'm trying to justify to myself why
|F(a)| > |F(b)| > |F(c)|
I think I can see why
|F(b)| > |F(c)|
due to special relativity case c observed from
the charges point of view would observe
the charges closer due to lorentz
contraction. As the charge is invariant would
result in a greater force?
However I can't justify to myself why
|F(a)| > |F(b)|
many thanks