rwooduk
- 757
- 59
... electron transport.
1. Homework Statement
Electron - Phonon scattering, derive the contribution to electron transport.
Trig.
Am I being REALLY stupid here, I can't see how the equation matches the triangle.
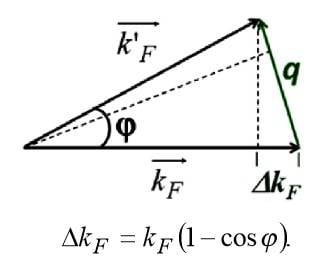
If you resolve KF' doesn't KF' cos theta= KF
The only thing I can think is that it's an approximation and delta KF is very small?
Thanks for any help
1. Homework Statement
Electron - Phonon scattering, derive the contribution to electron transport.
Homework Equations
Trig.
The Attempt at a Solution
Am I being REALLY stupid here, I can't see how the equation matches the triangle.
If you resolve KF' doesn't KF' cos theta= KF
The only thing I can think is that it's an approximation and delta KF is very small?
Thanks for any help