Electrostatics problem involving a Cone

[Tanya Sharma]

Homework Statement

A cone made of insulating material has a total charge Q spread uniformly over its sloping surface. Calculate the energy required to take a test charge q from infinity to apex A of cone. The slant length is L.

Homework Equations

The Attempt at a Solution

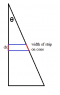
Potential at the tip of the cone is calculated by adding potentials due to rings of charges .

Let us consider a ring having charge 'dq' at a distance 'x' from the tip and at slant height L'. L'=xsecθ where θ is the half angle of the cone .

The surface area dS of the ring = 2π√(L'²-x²)dx

dq=Q(dS)/(πRL)

V = ∫dV = ∫kdq/L'

This doesn't give me correct answer .I am not sure if I have approached the problem correctly.

I would be grateful if somebody could help me with the problem.

 

[TSny]

The surface area dS of the ring = 2π√(L'²-x²)dx

Hello, Tanya. How "wide" is the ring on the surface of the cone? Is it dx?

 

[ehild]

I can not follow your notations. What are x and L'?

ehild

 

[Tanya Sharma]

How "wide" is the ring on the surface of the cone? Is it dx?

Hi TSny

The width is dxsecθ .That gives correct answer .

But I am having difficulty in comprehending (rather visualizing ) the difference between using dx and dxsecθ :shy:

My tiny brain can't differentiate between the two .I think if I use 'dx' then I am essentially covering the surface area of a cylinder ,not a cone . Am I right ?

But how is surface area of ring given by (Perimeter)(slant height) ? What is the shape of the differential element ? Is the ring in the form of a cylinder or is it more like a frustum of a cone?

I can not follow your notations. What are x and L'?

ehild

'x' is distance of the center of the ring from the tip and L' is distance between the tip and a point on the circumference of the ring.

 

[BvU]

You can help your brain by imagining a much bigger θ. Clearly no cylinder, hence the secθ.

 

[ehild]

'x' is distance of the center of the ring from the tip and L' is distance between the tip and a point on the circumference of the ring.

No need the centre of the ring mix in. The charge is distributed along the surface.
You get a circular section when you unroll the side of the cone. The centre of the circle is the tip of the cone. Can you see how to get the distance of a surface point from the tip? Do you see how to get the area of a ring?

ehild

 

[Tanya Sharma]

No need the centre of the ring mix in. The charge is distributed along the surface.
You get a circular section when you unroll the side of the cone. The centre of the circle is the tip of the cone. Can you see how to get the distance of a surface point from the tip? Do you see how to get the area of a ring?

ehild

Thanks ehild

Please have a look at the attachment .I have edited your diagram .Have I represented the ring (in red) correctly ?

 

[ehild]

That "ring" is not a ring really but part of the cone surface. You do not need x at all. Let be l the distance of a point on the surface of the cone from the tip. The unrolled cone has the central angle Φ=2πr/L. Then the surface element is lΦ dl. The area of the side of the cone is A=L²Φ/2.

ehild

 

[Tanya Sharma]

Hello TSny...

Could you please respond to post#4 and post#7 .

I am still not very clear how dxsecθ is the width of the ring.I understand it is more of a calculus concept . But if you could give your views , that would be very helpful .

 

[TSny]

Does the attached diagram help? If you "unwrapped" the strip off of the cone, it would be approximately a rectangle of width as shown in the diagram and length equal to the circumference of the circular cross section of the cone at the location of the strip.

 

[nnegi4545]

It goes like this.
Since u assumed an elementry part over the sloping surface , u must be inegrating over the surface .
So,
Instead of using dS= 2π√(L'2-x2) dx
U must use dS=2π√(L'2-x2) dl.
Hope u understood. This will give u correct answer.