Energy conservation paradox for constrained mass

[Fantasist]

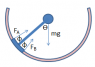
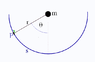
Consider the following setup (see illustration above): a mass m is connected to a circular section of a rail by means of a rod (with negligible mass) of length r, where r is the radius of the rail. The connection point P of the rod can move frictionless along the rail but is mounted such that the rod is always perpendicular to the rail, i.e. the mass is always at the center of the rail circle.
The rail is fixed to the ground and the mass subject to gravity. Initially, the rod is vertical (i.e. the weight of the mass fully supported by the rail). Now we push the rod along the rail until it is horizontal. The question is what work has to be done to do this? Let's see. The component of the gravitational force acting along the rail is given by

F(\theta) = m*g*sin(\theta)

where \theta is the angle from the vertical.
The work associated with moving the rod through an angle \pi/2 is then

W = \int F(s) ds = r*\int_0^\frac{\pi}{2} F(\theta) d\theta = m*g*r*\int_0^\frac{\pi}{2}sin(\theta) d\theta = m*g*r

This means the work required to move the rod from the vertical to the horizontal corresponds to the work of lifting the mass trough a height difference r. However, the mass m has always stayed in the same location, so no work against gravity was done at all.

How is this paradox resolved?

 

[jaytech]

I don't see how this is paradoxical. The mass never moved from the center, and therefore did no work. It is still located at mgr. I think you are confusing the path taken by the mass at the center with the path taken by the rod.

If the rod were not mass-less, then work would have been done by the rod's contribution to the system's energy. Work-Energy theorem states the projection of a force on a path is equal to the work. The mass at the center is not traversing a path, and hence there is no projection beyond the point where the rod is vertical.

If however, you were to hang the mass from the rod so the rod was attached to a ceiling, you would have the mass at the center performing work. It would follow the path of a simple pendulum.

 

[tiny-tim]

Hi Fantasist!

The component of the gravitational force acting along the rail …

Sorry, but this is meaningless …

the gravitational force acts through the mass m, and has nothing to do with the rail.​

(If you mean the reaction force, it is always perpendicular to the frictionless rail, and so does no work.)

 

[AlephZero]

If the system can remain in equilibrium for any value of $\theta$, your force $F(\theta)$ must correspond to the static friction between the rod and the rail.

When you move the rod, you do work against the friction force. End of paradox.

But I predict this thread will end up like https://www.physicsforums.com/showthread.php?t=731402

 

[Fantasist]

If the system can remain in equilibrium for any value of $\theta$, your force $F(\theta)$ must correspond to the static friction between the rod and the rail.

When you move the rod, you do work against the friction force.

It is assumed there is no friction (I have edited my post above in this sense). Clearly in this case the system can not stay in equilibrium for $\theta >0$ unless you apply an appropriate force along the rail at the connection point P. So in order to bring the rod from the vertical to the horizontal you have to apply work.

 

[jaytech]

You may be moving the rod, but no work is being done. The rod is massless and does not contribute to the energy. Only the central mass has mass and it isn't moving.

 

[Fantasist]

Hi Fantasist!


Sorry, but this is meaningless …

the gravitational force acts through the mass m, and has nothing to do with the rail.​

The mass is connected to the rail via the rod.

 

[Fantasist]

You may be moving the rod, but no work is being done. The rod is massless and does not contribute to the energy. Only the central mass has mass and it isn't moving.

The rod itself is massless, but it carries the full weight of the mass m. And this weight is not fully supported anymore by the rail if you move the rod out of the vertical. So you need to apply an additional force to support the mass m.

 

[tiny-tim]

Sorry, but this is meaningless …

the gravitational force acts through the mass m, and has nothing to do with the rail.​

(If you mean the reaction force, it is always perpendicular to the frictionless rail, and so does no work.)

The mass is connected to the rail via the rod.

so what?

the weight of the mass acts only on the mass

how can the weight of the mass act on the rail?

 

[Fantasist]

so what?

the weight of the mass acts only on the mass

how can the weight of the mass act on the rail?

See my previous post.

 

[jaytech]

What everyone in this thread is saying is that due to the position of the rod (BELOW the mass at the center), and the fact that the rod is massless, the rod is not producing any kind of force. This diagram at all points is equivalent to the mass at the center "floating" in midair.

 

[tiny-tim]

you are fundamentally misunderstanding what it means for a force to act on a body

there are two forces acting on the mass:

i] its weight, mg vertically down
ii] the reaction force from the rod, mg vertically up​

these forces balance, and so the mass stays where it is

there are three forces acting on the rod:

i] its weight, which we can take to be zero
ii] the reaction force from the mass, mg vertically down
iii] the reaction force from the rail, acting radially​

these forces do not balance, and so the rod moves

 

[Khashishi]

If the rod has no mass, then it takes no force to move the rod.

 

[sophiecentaur]

Isn't there a moment about the outer end of the rod (due to the fixing on the rail)? This will produce a force at the mass end of the rod which, along with the normal force, would produce a force equal and opposite to the weight.

 

[nasu]

To OP:
You assume that a tangential force is necessary to move the bar "up", in horizontal position.
But think it the other way. If the bar is initially horizontal, at rest, and you let it go will it "fall" in vertical position? Why would it do this? The potential energy does not change if it moves a little down the rail, does it? Of course, I mean in the conditions imposed in the scenario.

You made up a system whose potential energy is the same for any configuration. And which can have no kinetic energy. Like a massless ball on a horizontal surface. Try to apply a force to this and see what happens.

 

[Dale]

The component of the gravitational force acting along the rail is given by

F(\theta) = m*g*sin(\theta)

I assume that this is the force which resists moving the stand along the loop? If so, then its value is clearly 0.

 

[willem2]

I assume that this is the force which resists moving the stand along the loop? If so, then its value is clearly 0.

The rail must certainly exert a force mg in an upwards direction on the rod, to keep the rod and the mass from moving. That force has a component mgsin\theta in the direction of the rail that is not 0.

At first sight it looks impossible that the frictionless rail could exert such a force. The solution is that the part of the rod in contact with the rail must have a finite length to keep the mass from falling. The force from the rail on the upper part of the rod will be in a different direction than the force on the bottom part, so the sum of those forces can have a component that is in the direction of the rail at any point where the rod touches it.

 

[BruceW]

If the rod has no mass, then it takes no force to move the rod.

I assume that this is the force which resists moving the stand along the loop? If so, then its value is clearly 0.

yeah, exactly. The mass in the middle is supported due to tension in the rod, which ultimately comes from the fact that the end of the rod is fixed to the rail. If we move the rod along the rail, we are not moving the mass in the middle, and therefore we do no work. In this situation, we could only do work by a) accelerating the mass, or b) moving the mass through a gravitational field. In this case, the only mass is the mass in the middle, and it is staying in the same place, so no work is done.

It does seem weird. But there is no paradox. It seems weird because the rod is assumed to be very light, and also able to carry high tension (and stresses, when the rod is moved to be non-vertical). Intuitively in real life, if we see something which can carry large stresses, it is usually quite heavy as well. (except maybe spider silk).

 

[A.T.]

The solution is that the part of the rod in contact with the rail must have a finite length to keep the mass from falling. The force from the rail on the upper part of the rod will be in a different direction than the force on the bottom part, so the sum of those forces can have a component that is in the direction of the rail at any point where the rod touches it.

Yes, and this is basically the same issue as in the previous thread.

 

[Dale]

The rail must certainly exert a force mg in an upwards direction on the rod, to keep the rod and the mass from moving. That force has a component mgsin\theta in the direction of the rail that is not 0.

Agreed, but we are not interested in that force. We are interested in the additional external force that must be applied to rotate the rod. That force is clearly 0.

At first sight it looks impossible that the frictionless rail could exert such a force. The solution is that the part of the rod in contact with the rail must have a finite length to keep the mass from falling. The force from the rail on the upper part of the rod will be in a different direction than the force on the bottom part, so the sum of those forces can have a component that is in the direction of the rail at any point where the rod touches it.

Yes. For concreteness, let's assume that the structure consists of two pairs of frictionless ball bearings, each located an angle of $\phi$ away from the angle of the rod which is itself at an angle $\theta$ from the vertical. Then the forces at the bearings are:
$F_A=-mg \csc(2\phi) \sin(\theta-\phi)$
$F_B=mg \csc(2\phi) \sin(\theta+\phi)$

Each of these forces individually has no component tangent to the constraint, but because they are not parallel to each other, their sum cancels out both of the components of the gravitational force. Those forces are constraint forces and do not require any work, and neither oppose any external force attempting to rotate the rod.

 

[Dale]

If the system can remain in equilibrium for any value of $\theta$, your force $F(\theta)$ must correspond to the static friction between the rod and the rail.

When you move the rod, you do work against the friction force. End of paradox.

This is correct. The only work done in this case is against friction. As the friction goes to 0, so does the work.

I think that the confusion he has is not understanding that the system could be in equilibrium with no friction and non-zero $\theta$.

 

[sophiecentaur]

If there is no elastic energy stored in the system and the rod is massless then the GPE of the mass does not change so no work can be done.
This is the sort of problem you get when you try to combine ideal components in a situation and then try to treat it as if it's non-ideal. There are a million such phoney paradoxes.
You get the same thing with mathematical 'proofs' that 1=2 etc. etc.

 

[russ_watters]

Google: "one spoke wheel"

 

[Fantasist]

we could only do work by a) accelerating the mass, or b) moving the mass through a gravitational field. In this case, the only mass is the mass in the middle, and it is staying in the same place, so no work is done.

That is undoubtedly true for a free, unconstrained mass (where the work is done directly on the mass itself), but in this case the mass is externally constrained, and the state of the mechanical system can only change by moving the piece connecting the rod with the rail along the latter.
You have to remember that potential energy of a system is defined as work done over a path that changes the state of the system. But this may not necessarily imply that this change involves a movement of the mass. Saying that no work is done because the mass stays in place would be a circular conclusion in general.

 

[Fantasist]

At first sight it looks impossible that the frictionless rail could exert such a force. The solution is that the part of the rod in contact with the rail must have a finite length to keep the mass from falling.

What do you mean by 'keep the mass from falling'? Preventing the rod from breaking off? Just assume (for the sake of this argument) that the material is strong enough so that everything keeps intact even for an infinitesimally small contact area. Such an assumption is just part of the constraint.

 

[Fantasist]

For concreteness, let's assume that the structure consists of two pairs of frictionless ball bearings, each located an angle of $\phi$ away from the angle of the rod which is itself at an angle $\theta$ from the vertical. Then the forces at the bearings are:
$F_A=-mg \csc(2\phi) \sin(\theta-\phi)$
$F_B=mg \csc(2\phi) \sin(\theta+\phi)$

Each of these forces individually has no component tangent to the constraint, but because they are not parallel to each other, their sum cancels out both of the components of the gravitational force. Those forces are constraint forces and do not require any work, and neither oppose any external force attempting to rotate the rod.

1) How did you arrive at your equations for $F_A$ and $F_B$?
2) Why do the equations for $F_A$ and $F_B$ have different signs, but in your drawing the vectors point essentially in the same direction?
3) Why do your equations not depend on the length of the rod? Surely it should make a difference for your argument if e.g. the rod is shorter than the radius of curvature of the rail.

As it is, your argument is less than clear.

 

[A.T.]

Saying that no work is done because the mass stays in place would be a circular conclusion in general.

No work is done, because there is no force parallel to displacement.

What do you mean by 'keep the mass from falling'?

The weight of the mass must be balanced, if the mass stays static.

 

[A.T.]

Why do the equations for $F_A$ and $F_B$ have different signs, but in your drawing the vectors point essentially in the same direction?

Arrow directions usually just indicate the positive direction. The sign of the force then tells you the actual direction of the force, with respect to that convention.

Surely it should make a difference for your argument if e.g. the rod is shorter than the radius of curvature of the rail.

In your problem statement you made them equal.

 

[sophiecentaur]

1) How did you arrive at your equations for $F_A$ and $F_B$?
2) Why do the equations for $F_A$ and $F_B$ have different signs, but in your drawing the vectors point essentially in the same direction?
3) Why do your equations not depend on the length of the rod? Surely it should make a difference for your argument if e.g. the rod is shorter than the radius of curvature of the rail.

As it is, your argument is less than clear.

Because the same forces would apply whatever the radius of the circle. All circles are similar figures.

 

[BruceW]

That is undoubtedly true for a free, unconstrained mass (where the work is done directly on the mass itself), but in this case the mass is externally constrained, and the state of the mechanical system can only change by moving the piece connecting the rod with the rail along the latter.
You have to remember that potential energy of a system is defined as work done over a path that changes the state of the system. But this may not necessarily imply that this change involves a movement of the mass. Saying that no work is done because the mass stays in place would be a circular conclusion in general.

Work is either done to be stored as potential energy, or to be given to the kinetic energy of some matter. When the rod moves along the rail, no potential energy is stored, and no kinetic energy is gained by any matter. Therefore, you do zero work to move the rod. simples :) Maybe you would call this a circular conclusion, but I would call it self-consistent physics. The work-energy principle for a point-like mass is:
Work = \int_{t1}^{t2} \vec{F} \cdot \vec{v} dt
And in this case, it is zero, because the only significant mass is the one in the middle, which has zero velocity for all time. Further, the work done to store potential energy is simply equal to the potential energy stored. And in this case, we're implicitly assuming no potential energy is stored, since the rod is inelastic and cannot be deformed. Therefore, there is zero work converted to potential energy. So overall, no work is done.