bugatti79 said:
I created a jpeg of size 145KB which is under 195KB for a jpeg but it still won't load up.
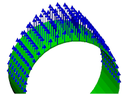
1) It is 7 nodes long
2) Distributing the force circumferentially over 7 nodes and axially over 7 nodes thereby giving total number of 49 nodes
How are they spaced physically?
3)Axis is z, correct
4)The total force is acting upwards, ie at 90degrees ACW.
What does ACW stand for? Is the force, then, always in the $+z$ direction?
I want to distribute this force circumferentially so that at angles 0 and 180, the force is 0, then repeat these forces axially 7 times.
5)We could call y our total force Fr.
So, $1/7$ of your total force is at each of the seven $z$ values, correct? Then you have seven locations around the circumference, presumably equally distributed, where the force is located. Are you treating each location here as a point force? In other words, is the force only at the node, or is it continually varying through all the degrees? If the force is to be treated as only occurring at the node, then where are the nodes, precisely? Is there one at $\theta=0^{\circ}$? Are they evenly spaced around the circumference?
So, I think I know the answers to your questions above. Proceeding on these assumptions, I am picturing a cylinder, $7$ nodes high and $7$ nodes around. You must distribute a force $F_r$ amongst these nodes such that $F_r/7$ is distributed at each $z$ value, and that $F_r/7$ at each $z$ value is distributed circumferentially such that the force is $0$ at angles $0^{\circ}$ and $180^{\circ}$.
So the trig function that does this is the $\sin(\theta)$ function. At least, it's zero at the right places. The problem is that it goes negative in the third and fourth quadrants. One way to fix this is simply to square it. So, let's take $\sin^{2}(\theta)$ as our starting point for getting the angle correct. We now need to ensure that
$$A\sum_{j=0}^{6}\sin^{2}\left(\dfrac{2\pi j}{7}\right)=\dfrac17.$$
Mathematica says that
$$\sum_{j=0}^{6}\sin^{2}\left(\dfrac{2\pi j}{7}\right)=
2\left[\cos^2\left(\dfrac{\pi}{14}\right)+\cos^2\left(\dfrac{3\pi}{14}\right)+\sin^2\left(\dfrac{\pi}{7}\right)\right].$$
It follows that
$$A=\frac{1}{14\left[\cos^2\left(\dfrac{\pi}{14}\right)+\cos^2\left(\dfrac{3\pi}{14}\right)+\sin^2\left(\dfrac{\pi}{7}\right)\right]}.$$
So, taken with the fact that the force must be directed in the $+z$ direction everywhere, we have that the force at any node ($z$ shouldn't enter into it) $\vec{F}$ is given by
$$\vec{F}=\frac{\hat{\mathbf{k}}\sin^{2}\left(\dfrac{2\pi j}{7}\right)}{14\left[\cos^2\left(\dfrac{\pi}{14}\right)+\cos^2\left(\dfrac{3\pi}{14}\right)+\sin^2\left(\dfrac{\pi}{7}\right)\right]},$$
where $0\le j\le 6$ is the number of the angle corresponding to the node.
Would this work for you?