Equation for the motion of an iron particle in a magnetic field

Click For Summary
SUMMARY

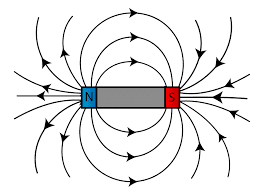
The motion of an iron particle in a magnetic field is governed by the principles of magnetic field density and force vectors. When placed between the poles of a stick-form magnet, the particle is attracted towards the area of highest field density, resulting in a trajectory that is not necessarily the shortest path. If the particle is positioned slightly off-center, it experiences a non-vertical force, causing it to approach the magnet at an angle rather than directly. The mathematical equation that describes this motion involves analyzing the magnetic field gradient and the resultant force vectors acting on the particle.

PREREQUISITES
  • Understanding of magnetic field theory
  • Familiarity with vector calculus
  • Knowledge of particle dynamics in physics
  • Basic concepts of magnetic field density
NEXT STEPS
  • Research the mathematical modeling of magnetic fields using Maxwell's equations
  • Study the Lorentz force law and its application to charged particles
  • Explore the concept of magnetic field gradients and their effects on particle motion
  • Learn about trajectory analysis in physics, particularly in non-uniform fields
USEFUL FOR

Physicists, engineering students, and anyone interested in the dynamics of particles in magnetic fields will benefit from this discussion.

ddddd28
Messages
73
Reaction score
4
Hello,
Let's assume we put a small iron particle in a magnetic field. What is the equation of the route that the particle performs? Is it the minimal route length that is possible? (the magnet is a stick-form)
upload_2017-2-1_17-37-49.png
 
Physics news on Phys.org
It might look that way, but I don't think so.

As a general rule, the particle will experience an attraction in the direction of the biggest field density increase. That however means for example, if you place it right in the middle between the poles but above the bar, all it will do is go straight towards the middle of the bar. But, if you place it slightly say to the right of that point, the direction of attraction will sightly point towards to the right because the field lines also get more dense towards that direction.

So, in essence, slightly off-center the particle experiences a non-vertical force, which will make it hit the bar at an angle. That then obviously is not the direct route.
 
I wanted to know which mathematical equation describes the route
 

Similar threads

Undergrad Origin of the Earth's magnetic field
  • · Replies 8 ·
Replies
8
Views
2K
High School Calculating Force on an Iron Object with Magnetic Field
  • · Replies 21 ·
Replies
21
Views
4K
Undergrad Is this analogy between Magnetic Force and Gravitational Force accurate in helping to understand what contributes more to a stronger magnetic force?
  • · Replies 11 ·
Replies
11
Views
2K
Undergrad Prevent a robotic cleaner from climbing on a block of iron with a magnet?
  • · Replies 8 ·
Replies
8
Views
2K
Undergrad Motional EMF in Faraday disc, co-rotating magnet axial mean flux
  • · Replies 5 ·
Replies
5
Views
656
Undergrad How can magnetic fields contain energy?
  • · Replies 17 ·
Replies
17
Views
3K
Undergrad Charge movement relative to magnetic field frame dependence/invariance
  • · Replies 5 ·
Replies
5
Views
1K
High School Circular motion as a result of the Lorentz force
  • · Replies 11 ·
Replies
11
Views
2K
Undergrad Magnetic field inside a capacitor
  • · Replies 16 ·
Replies
16
Views
2K
High School Seeing both B field lines and E field lines at the same time
  • · Replies 22 ·
Replies
22
Views
2K