Equilibrium : normal reaction of a rotational center?

[Doomski]

Homework Statement

I'm trying to figure out the reaction at D,that's where the system can rotate.

Problem:
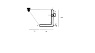
A force P of magnitude 90 N is applied to member ACDE, which is supported by a frictionless pin at D and by the cable ABE. Since the cable passes over a small pulley at B, the tension may be assumed to be the same in portions AB and BE of the cable. For the case when a=3m, determine:
a)the tension in the cable
b) the reaction at D

2. The attempt at a solution

I've calculated the tension in the cable through the sum of momentum=0, T= 117N. For the reaction, I used the sum of forces=0; We don't have the mass of the system, so I assumed there's three forces acting on D, a normal force and the weight of the system that cancel each other (probably wrong?) and the reaction. From that,I got R = 129.8N. Is that right?
Are there a difference between a normal reaction of a table, for example, and Rd ??

Thanks.

Edit: I had to paint the figure because the photo wasn't clear.

 

[haruspex]

I've calculated the tension in the cable through the sum of momentum=0, T= 117N

To get that, I have to assume the horizontal part of the L piece is weightless. Doesn't your method assume that?
To find the reaction at D, you will need to assume the same for the vertical part. You have three unknown scalars, tension and the components of the reaction force, and only three available equations. Any more unknowns make it unsolvable.
I agree with your answer.

 

[Doomski]

To get that, I have to assume the horizontal part of the L piece is weightless. Doesn't your method assume that?
To find the reaction at D, you will need to assume the same for the vertical part. You have three unknown scalars, tension and the components of the reaction force, and only three available equations. Any more unknowns make it unsolvable.
I agree with your answer.

Now that makes sense, thank you!