Equilibrium of a Homogeneous Dice on Horizontal Rods: Finding the Critical Angle

[jcdenton]

Hi !

I've been working on the following problem for quite some time now and I just can't figure out how to do it:
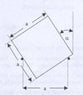
A homogeneous dice, whose edges have a length of a, is situated on two horizontal, thin, rigid rods. The rods are parallel to each other and are installed on the same height above the ground. Each of the rods is also parallel to one side of the dice. The coefficient of friction, μ, equals 0.2. For which angles α is the dice in a state of equilibrium ?
It is clear that the dice is in such a state for an angle α of 45°. However, due to friction, there must be additional angles, which are slightly bigger and smaller than 45°. But I do not know how to find these angles. I have tried to draw a diagram of all the forces involved in the problem, but I don't know which torques I need to consider and at which points I need to draw them.
It would be very nice if someone could help me solve this problem.

Thank you very much

Sebastian

 

[Bartholomew]

Some preliminary geometry

I did a bunch of triangulation and found two things you need:

1.) If the center of mass of the square is traced down to where it crosses the line between the two pegs, the distance from the left peg to that crossing is

(L + (L - L COS a) COS a) - (2 ^ .5 * L / 2 * SIN (a + PI/4))

And the distance from the right peg to that crossing is (L - distance to left peg).

I don't know how much that expression can be simplified--I didn't even try.

You need those distances to find how much of the weight rests on each peg--it's not an equal split except when "a" is 45 degrees.

I'm going to call the distance from the left peg to the crossing X and the distance from the right peg to the crossing L - X so that I don't have to say that whole thing out again.

2.) First, the distance from the center of the square to the crossing is

(2 ^ .5 * L / 2 * SIN (a + PI/4)) - L * COS a SIN a

I will call that distance Y.

The distance from the left peg to the center of mass is therefore

(X ^ 2 + Y ^ 2) ^ .5

and the distance from the right peg to the center of mass is

((L - X) ^ 2 + Y ^ 2) ^ .5


Those two distances are your lever arms.

 

[jcdenton]

Hi !

@Bartholomew: Thank you very much for your efforts. Even though I haven't yet completely understood your calculations, they surely have provided me with a clou of how this problem might be solved. I'll continue working on it.

Thank you again

Sebastian