VictorWutang
- 13
- 0
Homework Statement
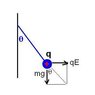
A small positively charged sphere of mass m is attached to a very large positively charged vertical plate by a string and hangs due to gravity. The charge density on the plate, σ, is uniform.
a) Calculate the equilibrium position of the ball as a function of the (uniformly distributed) charge on the ball. I.e. what angle does the string make with the vertical?
b) estimate the capacitance between the sphere and the plate.
Homework Equations
F = kqσ / r2 (not sure if this is correct)
E = kq / r
The Attempt at a Solution
a) Pythagorean theorem will come into use. I have to find where the force due to the magnetic field of the plate is equal to the force of gravity resisting it, but I can't figure out how to make the force of gravity,the force of the electric field and the tension/normal force to be in vectors that cancel out. More specifically, i can't figure out how to express the downward force of gravity to be perpendicular to the plate to cancel out the force from the plate.
b) once i find this distance, capacitance will just be ε0*A / d with A being ∏r2 with r being the radius I would estimate the ball to be.