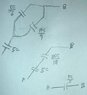
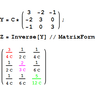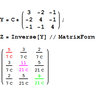jishnu said:
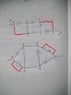
This is how I got the answer(attached a rough work)
Can you please provide me resources to know more about formation of the admittance matrix, I couldn't understand much relevant things about its matrix formation from the electronics tutorial link that you have provided.
View attachment 227195
'
When using the Y-Δ transformation:
https://en.wikipedia.org/wiki/Y-Δ_transform
the elements of the circuit must be treated as resistances (impedances in our case), not conductances (admittances in our case). We have taken the capacitances to be admittances because of the way capacitors combine when they are in parallel, and when in series. When capacitors are in parallel, their values are simply added. This is not the way resistors (or inductors) in parallel combine.
So for the purpose of this exercise, we treat the admittance of a capacitor whose value is 2C as if it were an admittance of value 2C, or an impedance of value 1/(2C). If we want the equivalent capacitance of two capacitors 2C and 3C in parallel, it's just 5C. But, if they're in series, we must calculate 1/Ceqv = 1/(2C) + 1/(3C), which gives Ceqv = (6C)/5
For capacitors in series, add their impedances; for capacitors in parallel, add their admittances.
When using the Y-Δ transformation be sure to have the values used in the calculation in impedance form, not admittance form.
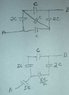
Here are the steps for the solution of the new circuit I gave you using the Y-Δ transformation. In these images the values shown are in admittance form. Even though it's not shown, to use the transformation I took the reciprocals to convert them to impedances before doing the calculations. The results were then converted back to admittance form by taking reciprocals.
Notice how nicely the nodal analysis method with the nodal equations in matrix form took care of all the reductions and algebra automatically.
Regarding more information about the admittance matrix, search on Google for the phrase "admittance matrix by inspection". Also look for "nodal analysis".